Design variations and hierarchical layout
The next step is to use the MZI PCell defined in the previous section to create a sweep of MZIs with different lengths of the right arm.
For this case, we will also use i3.Circuit to easily simulate each MZI that is part of our design to check their behavior.
When submitting designs to a foundry, more often than not you are allowed limited space to fit your designs.
To make sure that the design is not bigger than the allowed area, it is useful to use a frame.
The Luceda PDK for SiEPIC contains a PCell called FloorPlan, which can be used exactly for this purpose.
The height and width of this PCell can be adjusted according to your requirements.
In this tutorial, we are going to use the floorplan to make sure the three MZIs don’t exceed our design area.
Let’s now have a look at how we can define design variations using IPKISS. Open the file “example_design_variations.py” in your PyCharm project, so that you can follow along the explanation.
Parameters for the MZI sweep
First of all, we define the parameters that we will use for the MZI sweep.
We want to design three different MZIs.
The right arm of each MZI will pass through a different coordinate in order to control its length.
We provide this coordinate to the MZI PCell using the control_point property.
The following parameters are defined at the beginning of the file:
control_points: A list of coordinates [(x1, y1), (x2, y2), (x3, y3)] that will be used to instantiate the MZI PCells of the three MZIs we want to design.bend_radius: The waveguide bend radius we will use for our designs.x0andy0: The x- and y-coordinates where we will place the bottom left fiber coupler of the first MZI. They are defined to be a bit distant from the origin because the bottom left corner of the floorplan will be placed at the origin.spacing_x: The horizontal spacing between the fiber grating couplers of the three MZIs.
After defining these parameters, we create an empty insts dictionary and an empty specs list.
We will add to them all the cells that we want to instantiate and the placement specifications that we need to provide to i3.Circuit to create our final design.
# Parameters for the MZI sweep
control_points = [(70.0, 240.0), (100.0, 240.0), (150.0, 240.0)]
bend_radius = 5.0
x0 = 40.0
y0 = 20.0
spacing_x = 180.0
insts = dict()
specs = []
Floorplan
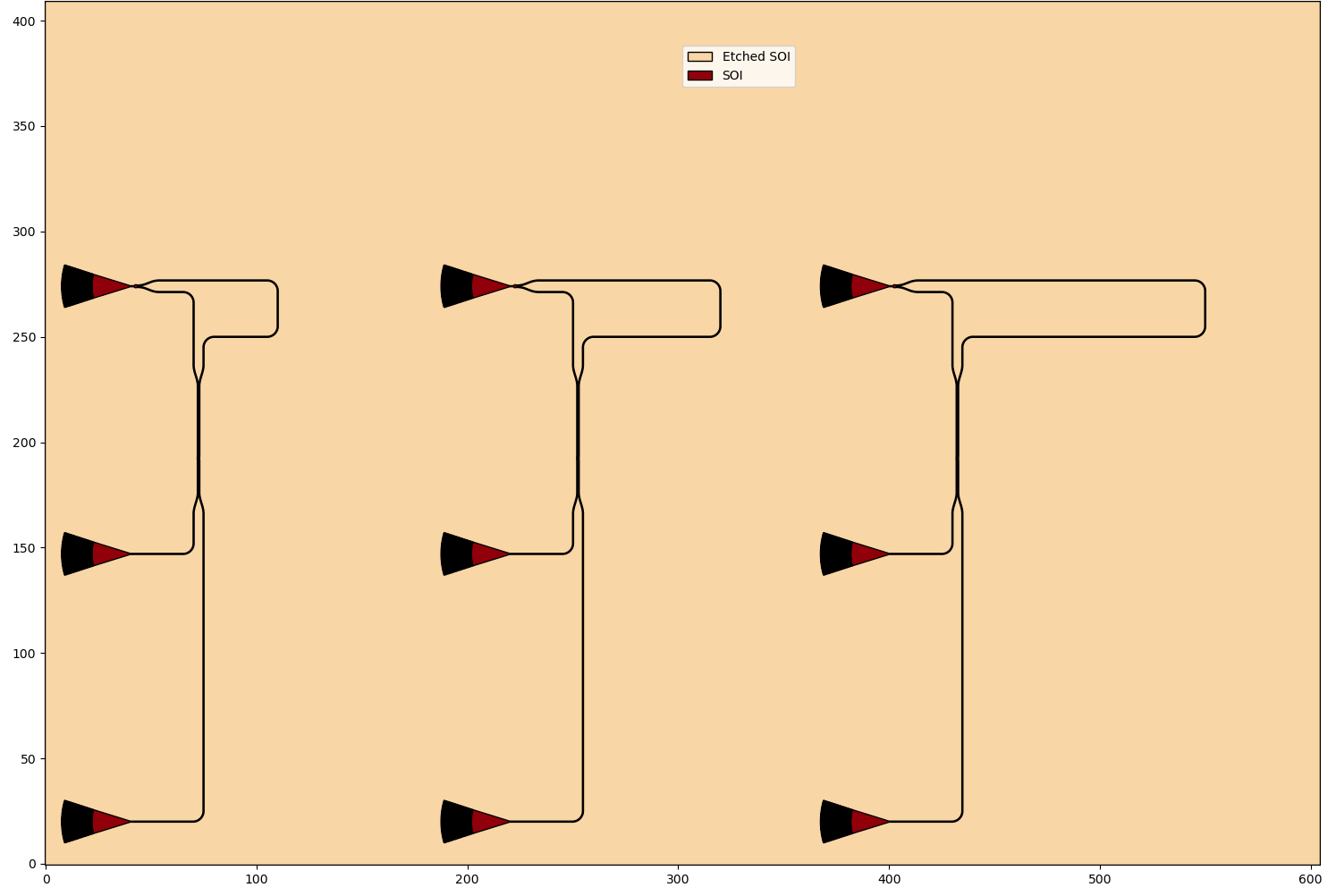
Before designing the MZIs, it is good to have clear what are the boundaries for our design. We instantiate the floorplan from the Luceda PDK for SiEPIC, we add it to the instances dict and we place the bottom left corner at the origin.
# Create the floorplan
floorplan = pdk.FloorPlan(name="FLOORPLAN", size=(605.0, 410.0))
# Add the floorplan to the instances dict and place it at (0.0, 0.0)
insts["floorplan"] = floorplan
specs.append(i3.Place("floorplan", (0.0, 0.0)))
MZI sweep
To create the MZI sweep, we use a practical for-loop over the list of control points.
Each time we instantiate an MZI with the correct control point, we add it to the dictionary of instances and place it at the coordinates (x0, y0).
For the first MZI, these are the coordinates we defined in the initial parameters.
For each following MZI, the value of x0 is increased by the value in spacing_x.
For our own reference, after each MZI is instantiated, we calculate the delay length between the two arms of the MZI and print it.
Very important!
Each time we instantiate an MZI, we have to assign a unique name.
Otherwise, the tree instantiated MZIs will be an exact copy of each other and changing the design of one of them will result in a change in all of them.
To make sure the names are all different, we use the for-loop counter ind to call them MZI0, MZI1, MZI2.
# Create the MZI sweep
for ind, cp in enumerate(control_points):
mzi = MZI(
name=f"MZI{ind}",
control_point=cp,
bend_radius=bend_radius,
)
# Calculate the actual delay length and print the results
right_arm_length = mzi.get_connector_instances()[1].reference.trace_length()
left_arm_length = mzi.get_connector_instances()[0].reference.trace_length()
delay_length = right_arm_length - left_arm_length
print(
mzi.name,
f"Delay length = {delay_length} um",
f"Control point = {cp}",
)
mzi_cell_name = f"mzi{ind}"
insts[mzi_cell_name] = mzi
specs.append(i3.Place(mzi_cell_name, (x0, y0)))
x0 += spacing_x
Final design
We now create our circuit to be simulated using i3.Circuit.
Most of the heavy work is done.
We only need to instantiate a circuit cell that contains the instances and the placement specifications that we carefully defined before.
# Create the final design with i3.Circuit
cell = i3.Circuit(
name="EBeam_chiara_v1",
insts=insts,
specs=specs,
)
Layout and circuit simulation
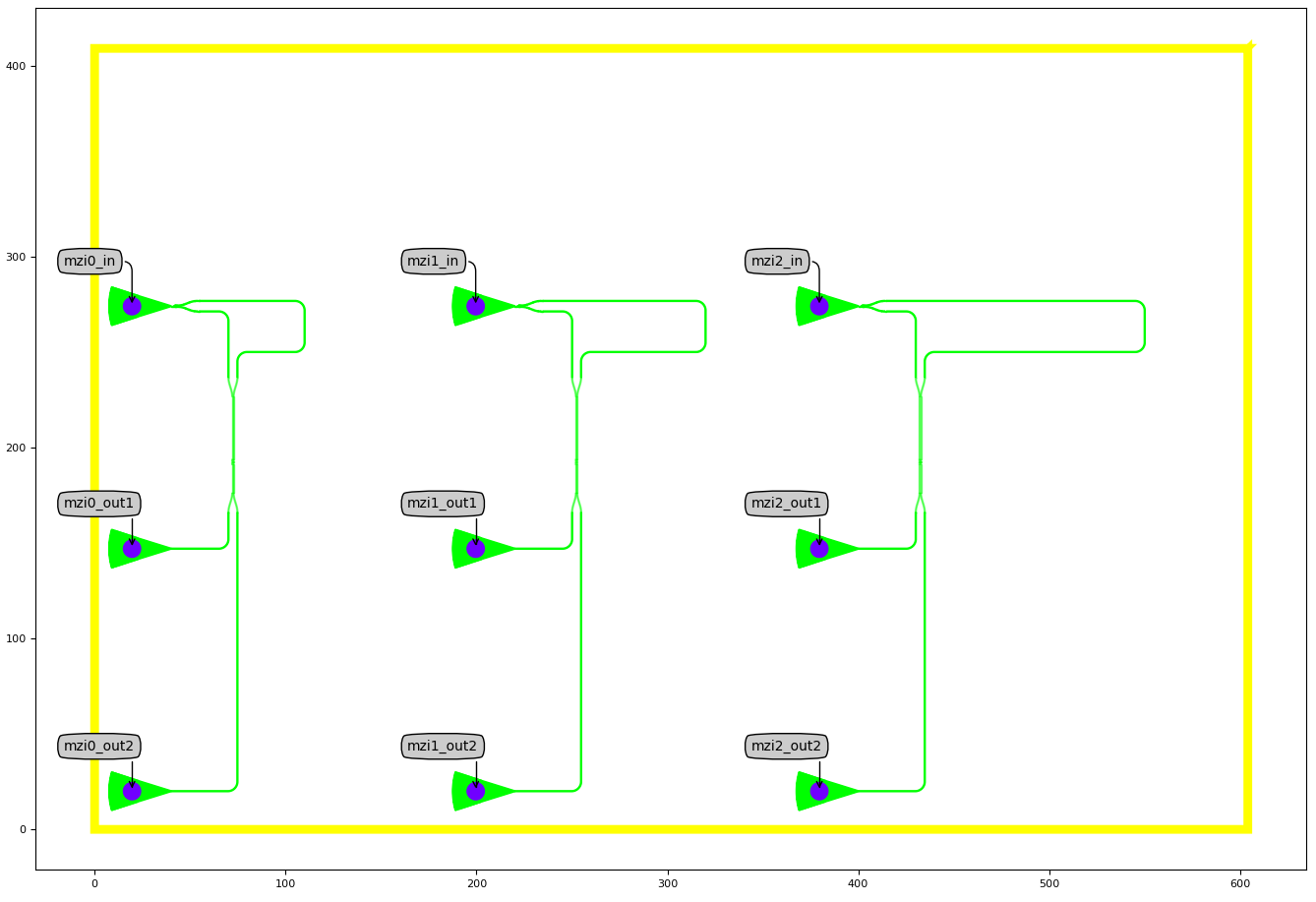
We can now instantiate the layout and save it to gds:
# Layout
cell_lv = cell.Layout()
cell_lv.visualize(annotate=True)
cell_lv.write_gdsii("EBeam_chiara.gds")
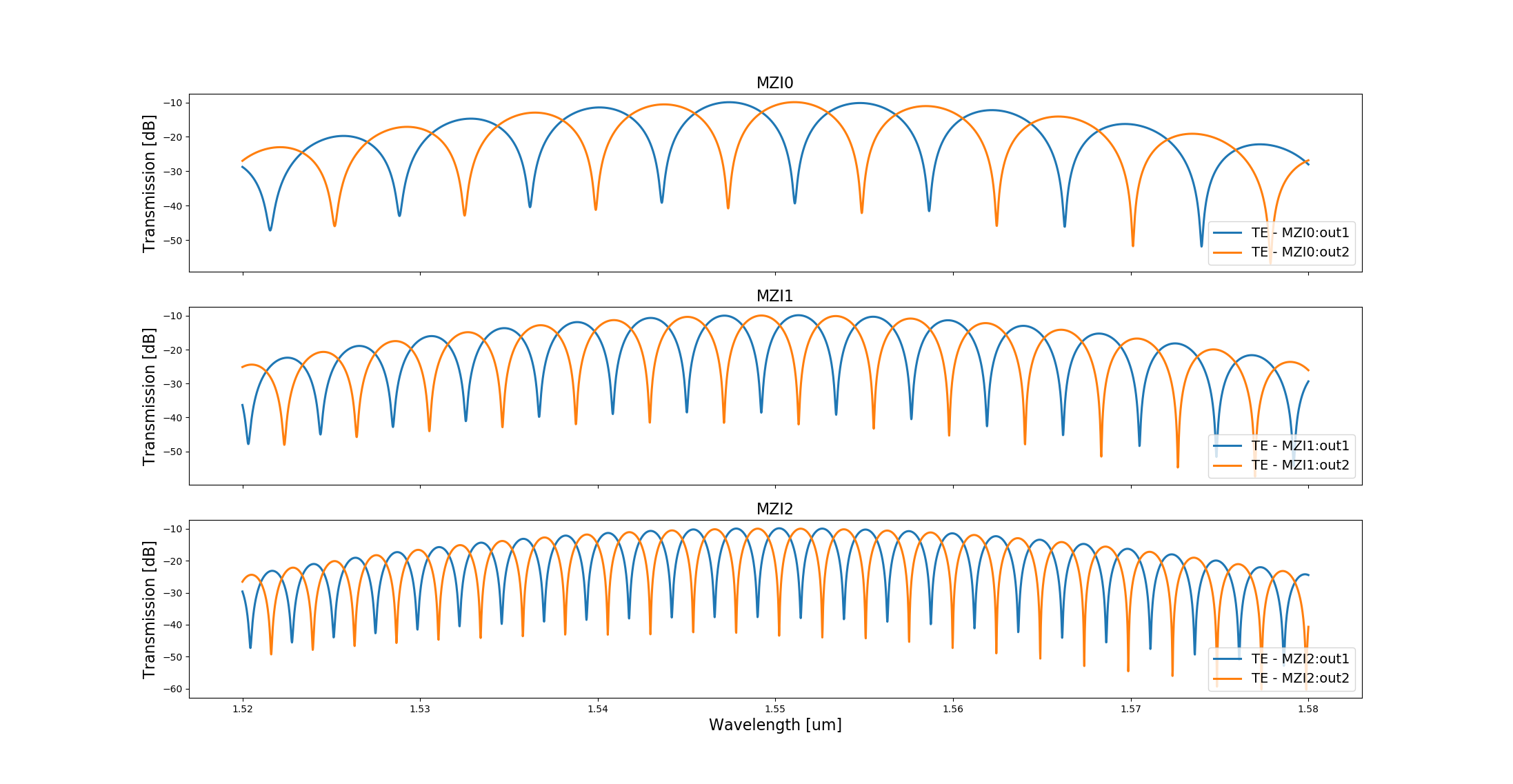
Next, we can extract the S-matrix and plot the results of the circuit simulation to visualize the behaviour of our MZIs:
# Circuit model
cell_cm = cell.CircuitModel()
wavelengths = np.linspace(1.52, 1.58, 4001)
S_total = cell_cm.get_smatrix(wavelengths=wavelengths)
# Plotting
fig, axs = plt.subplots(3, sharex="all")
for ind, cp in enumerate(control_points):
tr_out1 = i3.signal_power_dB(S_total[f"mzi{ind}_out1:0", f"mzi{ind}_in:0"])
tr_out2 = i3.signal_power_dB(S_total[f"mzi{ind}_out2:0", f"mzi{ind}_in:0"])
axs[ind].plot(wavelengths, tr_out1, "-", linewidth=2.2, label=f"TE - MZI{ind}:out1")
axs[ind].plot(wavelengths, tr_out2, "-", linewidth=2.2, label=f"TE - MZI{ind}:out2")
axs[ind].set_ylabel("Transmission [dB]", fontsize=16)
axs[ind].set_title(f"MZI{ind}", fontsize=16)
axs[ind].legend(fontsize=14, loc=4)
axs[2].set_xlabel("Wavelength [um]", fontsize=16)
plt.show()
print("Done")
Test your knowledge
Do these results satisfy your expectations? If not, change the control points to change the length of the right arm and check again the simulation.