PHIX ADK: IQ Modulator
In this tutorial, we will design a silicon photonic high-speed IQ modulator packaged using the Luceda Assembly Design kit for PHIX. The components are illustrated in the figure below.
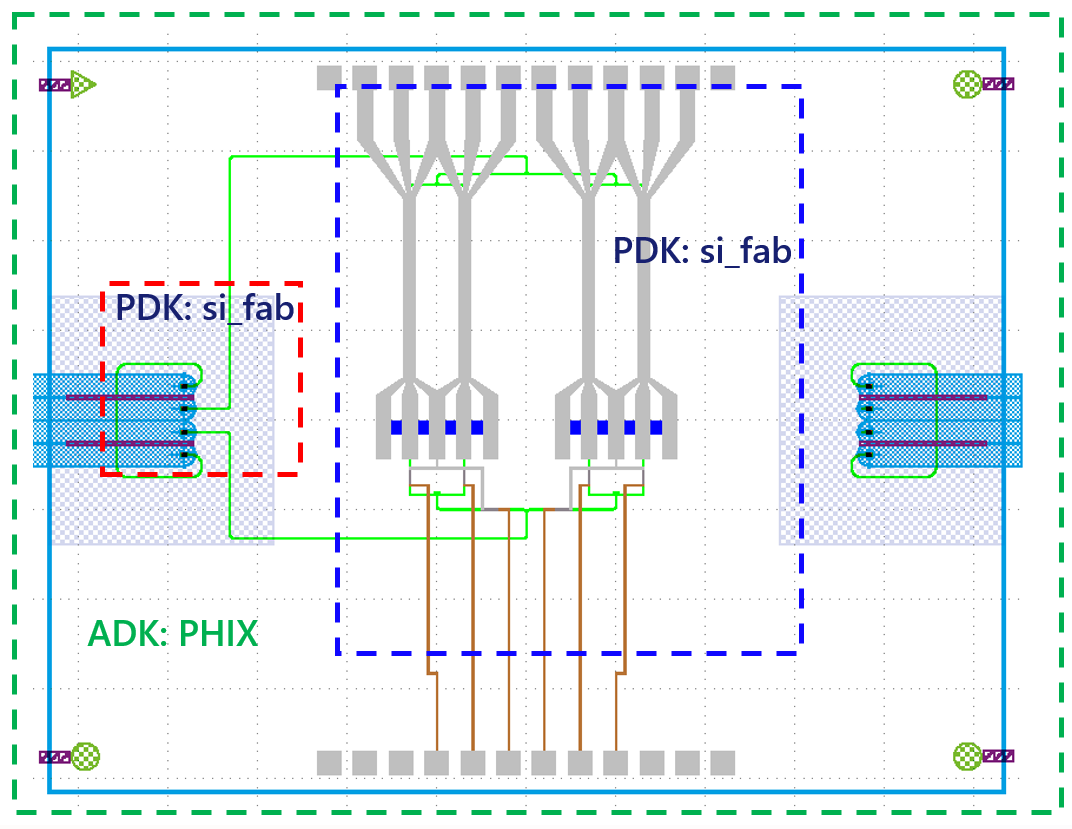
The design is based on elements from SiFab, Luceda’s demonstration photonics processs design kit (PDK), combined with custom components designed in a photonics team on top of this PDK and the packaging frame from the assembly design kit.
The code used to create this design and referenced in this tutorial can be found in your Luceda Academy project in luceda_academy/designs/iq_modulator.
Why we need an IQ Modulator
High speed modulation is essential for modern communications. High-bandwidth data transmission utilizes optical communication links due to orders of magnitude lower signal losses as compared with electrical signals. Electro-optic modulation is used to take an optical carrier wave and modulate it with an electrical signal. The details of this can be seen in our tutorial Mach-Zehnder modulator
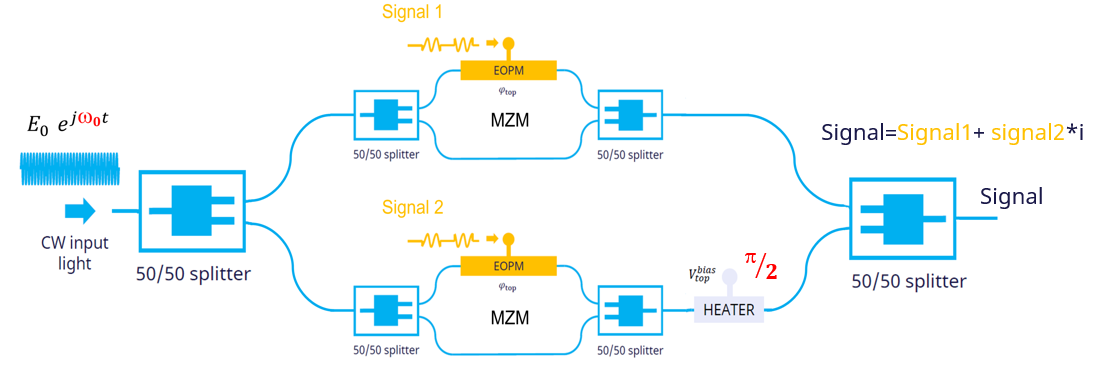
To implement a high-speed modulator, we convert phase modulated light into amplitude modulated light using an MZM. By combining two MZMs with 50/50 splitters at the input and output, it is possible to transmit two signals using one frequency thus significantly increasing the spectrum efficiency.
Fully assembled design
The GDSII file of the finalised design is generated by running the example_iqmodulator_packaged_layout.py file.
Let’s go through it step by step.
Step 1: Importing the Dependencies
In Luceda IPKISS, dependencies of your design are imported at the top of your code, just like you would do for any other Python module. In our case, we import the following dependencies:
SiFab PDK: SiFab is Luceda’s demonstration PDK emulating the technology of a traditional SOI foundry. Grating couplers, splitters and bondpads will be directly imported from here.
PHIX ADK: The Assembly Design Kit (ADK) for PHIX is a design kit for packaging a photonics IC using the PHIX Characterization Package. By using the ADK, it is a lot easier to adhere to the design rules that will enable you to package and measure your chip afterwards.
pteam_library_si_fab: Local component library containing components that are shared across different designs made by your photonics team.
IQ Modulator design: This design is defined in a separate file
iqmodulator_designs.pyand uses ingredients from the dependencies above to create the IQ modulator.Simulation of modulation schemes: Separate files are implemented for each modulation scheme.
import si_fab.all as pdk
from iqmodulator_designs import IQModulator, PackagedIQModulator
from pteam_library_si_fab.components.mzm.pcell.cell import MZModulator
Step 2: Instantiating the Phase Shifter and the Heater
After the import statements, we instantiate the phase shifter from the SiFab PDK with the desired length. For more information about this PCell and the parameters that can be set, check out the SiFab documentation: PhaseShifterWaveguide.
# Phase Shifter
ps = pdk.PhaseShifterWaveguide(
name="phaseshifter",
length=1000.0,
core_width=0.45,
rib_width=7.8,
junction_offset=-0.1,
p_width=4.1,
n_width=3.9,
Next we instantiate the heater that we are going to use for the MZM later.
# Phase Shifter (heater)
heater = pdk.HeatedWaveguide(name="heater")
heater.Layout(shape=[(0.0, 0.0), (100.0, 0.0)])
Step 3: Instantiating the MZM
The Mach-Zehnder modulator we will use in this tutorial is made of two arms, each with an electro-optic phase modulator and heater.
The design of the MZM is explained in details in the Mach-Zehnder modulator tutorial.
In step 1, we imported the MZM from the pteam_library_si_fab.components.mzm.pcell.cell
Now we instantiate the MZM and we pass the phase shifter we have instantiated above to the MZM , together with parameters to adjust the metal pads size and position.
# MZModulator
mzm = MZModulator(
phaseshifter=ps,
heater=heater,
rf_pad_width=75,
rf_pad_length=350,
rf_signal_width=5.0,
rf_ground_width=20.0,
rf_pitch_in=200,
)
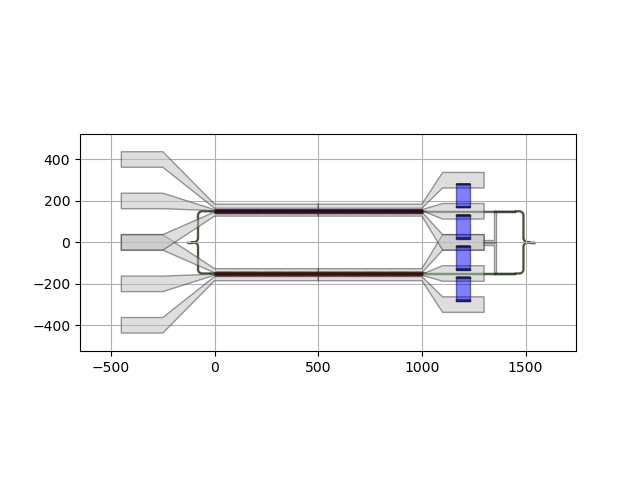
The MZM has the following layout.
Step 4: Instantiating the IQ Modulator
We next instantiate the IQ modulator by calling the IQModulator, which we have defined separately in the file iqmodulator_designs.py and imported at the top.
# IQ Modulator
IQ_mod = IQModulator(mzm=mzm)
Here we see the layout of the combined MZMs making an IQ Modulator.
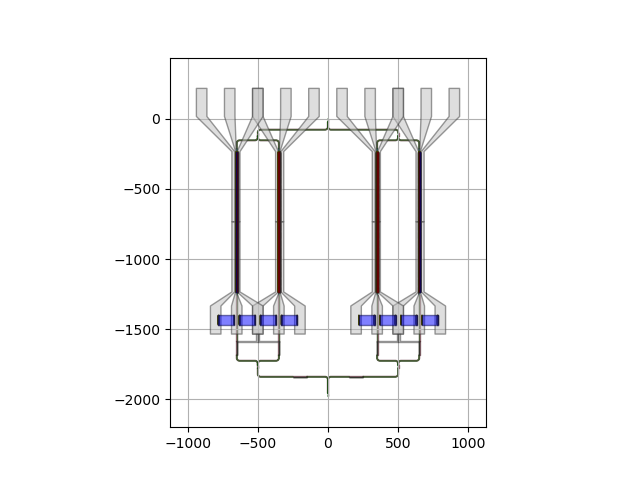
Step 5: Instantiating the PHIX ADK Packaging Frame
From the Luceda ADK for PHIX, we instantiate the packaged IQ modulator via the imported PackagedIQModulator from the iqmodulator PCell.
The file iqmodulator_designs.py contains the parameters we will use in this design from the PHIX Characterization Package.
The PHIX Characterization Package allows the designer to work in an efficient manner by setting constraints on the design from the beginning. It contains numerous parameters that have specific requirements or boundaries that must be adhered to.
The PHIX Characterization Package contains packaging considerations such as the grating type, the number of couplers, the epoxy area, the distance to the edge, bondpad sizes and various other parameters. In the following code, we see an example of how it can be implemented.
from phix.all import CharacterizationPackage
return CharacterizationPackage(
pic_length=5325,
pic_width=4150,
couplers_type=True,
couplers_number=4,
couplers_pitch=127,
pad_number=12,
pad_pitch=self.pad_pitch,
pad=self.bondpad,
marker_layer=i3.TECH.PPLAYER.M2,
pad_to_edge=100,
coupler=self.gc,
)
In this example, we use grating couplers by setting coupler_type = True.
The couplers_pitch = 127 which is one of two possibilities as defined in the ADK.
We also define the number of couplers, pads and the distance to to the pad edge.
We simply now instantiate the IQ modulator with the following function.
# Packaged IQ modulator
IQ_mod_packaged = PackagedIQModulator(
dut=IQ_mod,
)
The packaged layout of the IQ modulator can be seen here.
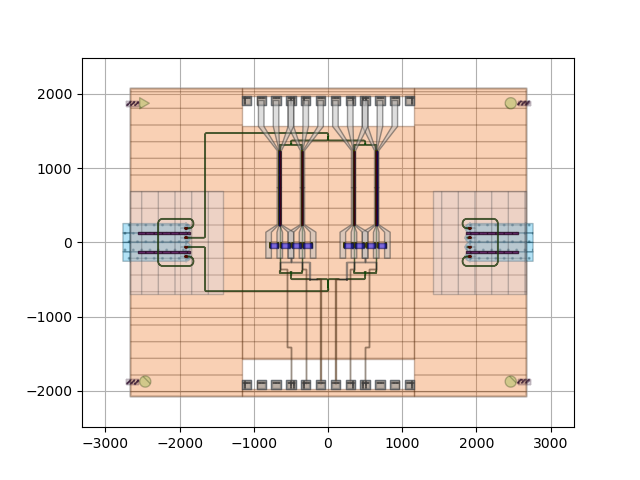
Step 6: Modulation Scheme Simulations
Modulation schemes are essential components of communication systems, enabling the efficient encoding of information onto carrier signals for transmission. By modulating parameters such as amplitude, frequency, or phase of the carrier signal, different modulation schemes offer varying degrees of spectral efficiency, robustness, and complexity. In this section we look at some common modulation schemes and how to simulate them in IPKISS.
On-Off Keying (OOK)
OOK is a simple modulation scheme in which the amplitude of the signal is modulated by varying the in-phase component of the IQ constellation diagram corresponding to “on” or “off” states.

We start by defining a simulation model for our MZM.
import random
import numpy as np
import ipkiss3.all as i3
from si_fab.benches.sources import random_bitsource, rand_normal
def simulate_modulation_mzm(
cell,
mod_amplitude=None,
mod_noise=None,
opt_amplitude=None,
opt_noise=None,
v_mzm1=None,
v_mzm2=None,
bit_rate=10e9,
n_bytes=100,
steps_per_bit=50,
center_wavelength=1.5,
debug=False,
Next, the excitations with noise in the optical and electrical domain are defined.
# Define the excitations with noise on the electrical
f_mod = random_bitsource(
bitrate=bit_rate,
amplitude=mod_amplitude,
n_bytes=n_bytes,
Finally, we define a testbench with connections and a testbench model with a circuit model. The results are returned from the time domain simulation.
testbench_model = testbench.CircuitModel()
results = testbench_model.get_time_response(
t0=t0,
t1=t1,
dt=dt,
center_wavelength=center_wavelength,
debug=debug,
)
return results
Having defined a simulation model for the MZM, we can import this into an OOK simulation file. We start by importing the necessary dependencies.
"""Simulate an MZ modulator working in OOK modulation format.
This script generates several outputs:
- visualize the layout in a matplotlib window (this pauses script execution)
- circuit simulation result (time-domain)
- Plot EyeDiagram
- Plot Constellation diagram
"""
import numpy as np
import matplotlib.pyplot as plt
import si_fab.all as pdk
from ipkiss3 import all as i3
from pteam_library_si_fab.components.mzm.pcell.cell import MZModulator
from simulation.simulate_mzm import simulate_modulation_mzm, result_modified_OOK
We then instantiate the phase shifter, heater and MZM.
# visualize the layout of MZM.
########################################################################################################################
# Phase Shifter
ps = pdk.PhaseShifterWaveguide(
name="phaseshifter",
length=1000.0,
core_width=0.45,
rib_width=7.8,
junction_offset=-0.1,
p_width=4.1,
n_width=3.9,
)
vpi_lpi = 1.2 # V.cm
cl = 1.1e-16 # F/um
res = 25 # Ohm
tau = ps.length * cl * res # Time constant associated with the modulator
ps.CircuitModel(vpi_lpi=vpi_lpi, tau=tau)
# heater
heater_length = 100
heater = pdk.HeatedWaveguide(name="heater")
heater.Layout(shape=[(0.0, 0.0), (heater_length, 0.0)])
heater_width = heater.heater_width * 2
p_pi_sq = heater.CircuitModel().p_pi_sq # Power needed for a pi phase shift on a square [W]
V_half_pi = np.sqrt(
np.pi / 2 * p_pi_sq * heater_length / (np.pi * heater_width)
) # Voltage needed for a half pi phase shift
V_pi = np.sqrt(np.pi * p_pi_sq * heater_length / (np.pi * heater_width)) # Voltage needed for a pi phase shift
# MZModulator
mzm = MZModulator(
phaseshifter=ps,
heater=heater,
rf_pad_width=75,
rf_pad_length=100,
rf_signal_width=5.0,
rf_ground_width=20.0,
rf_pitch_in=200,
)
In the heater section, we define some important parameters.
p_pi_sq = Power needed for a pi phase shift on a square [W]
V_half_pi = Voltage needed for a half pi phase shift
V_pi = Voltage needed for a pi phase shift
The power required for a \(\pi\) phase shift serves as a reference for determining the voltages needed to achieve \(\pi/2\) and \(\pi\) phase shifts in a MZM. These voltages are then applied to the arms of the MZM in a specific manner to generate the desired modulation scheme.
For On-Off Keying (OOK), a phase shift of \(\pi/2\) is applied to MZM1, while no voltage is applied to MZM2. This configuration results in the ‘on’ and ‘off’ states, effectively implementing the OOK modulation.
# Simulation of a MZM working in OOK modulation format.
########################################################################################################################
results = simulate_modulation_mzm(
cell=mzm,
mod_amplitude=3.0,
mod_noise=0.5,
opt_amplitude=1.0,
opt_noise=0.01,
v_mzm1=0.0, # MZM works at its linear biased point
v_mzm2=0.0,
bit_rate=50e9,
n_bytes=2**8,
steps_per_bit=2**7,
center_wavelength=1.55,
This section of code defines the simulation parameters. We see the modulation amplitude, noise, and voltages applied to MZM arms. The simulation then returns the signal, reversed signal, and voltages across the MZM arms.
Finally, it plots these outputs against time.
outputs = ["sig", "revsig", "mzm1", "mzm2", "src_in", "out"]
titles = [
"RF signal",
"RF reversed signal",
"Heater(bottom) electrical input",
"Heater(top) electrical input",
"Optical input",
"Optical output",
]
ylabels = ["voltage [V]", "voltage [V]", "voltage [V]", "voltage [V]", "power [W]", "power [W]"]
process = [np.real, np.real, np.real, np.real, np.abs, np.abs]
fig, axs = plt.subplots(nrows=len(outputs), ncols=1, figsize=(6, 10))
for ax, pr, out, title, ylabel in zip(axs, process, outputs, titles, ylabels):
data = pr(results[out][1:])
ax.set_title(title)
ax.plot(results.timesteps[1:] * 1e9, data, label="mzm")
ax.set_xlabel("time [ns]")
ax.set_ylabel(ylabel)
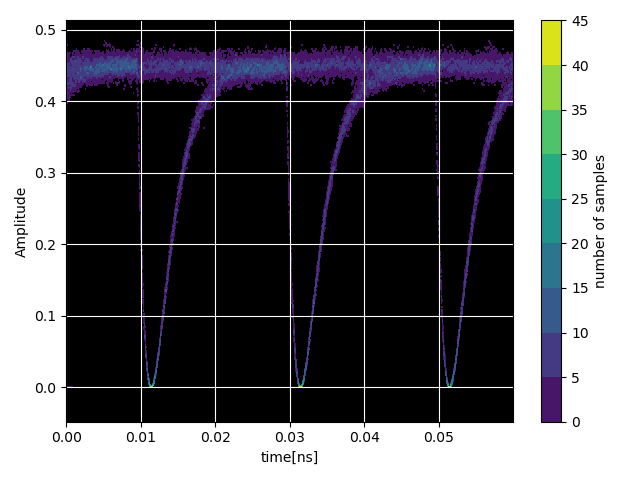
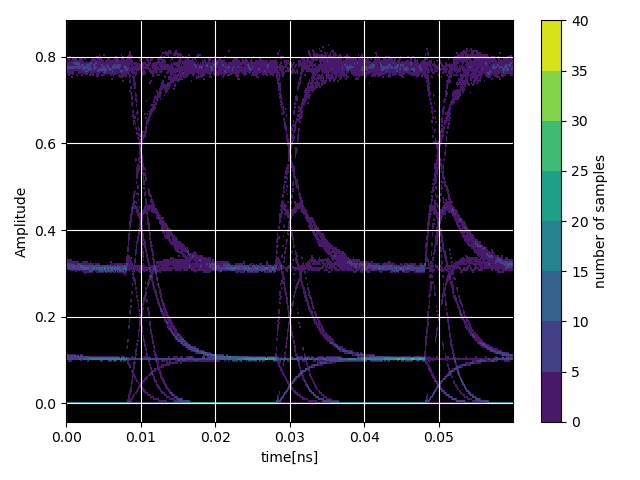
Extending this, we can visualize the simulations by implementing an eye diagram. An eye diagram is a graphical representation of a digital signal’s quality in a communication system. Multiple bits of a digital signal are plotted on top of each other, where each bit is represented by a pulse. An eye diagram is formed when these pulses are overlaid over multiple periods.
# Plot EyeDiagram
########################################################################################################################
num_symbols = 2**8
samples_per_symbol = 2**7
data_stream = np.abs(results["out"]) ** 2
baud_rate = 50e9
time_step = 1.0 / (baud_rate * samples_per_symbol)
eye = i3.EyeDiagram(data_stream, baud_rate, time_step, resampling_rate=2, n_eyes=2, offset=0.2)
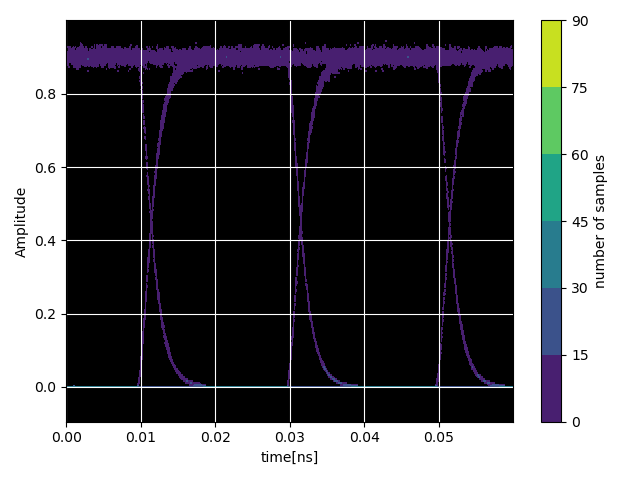
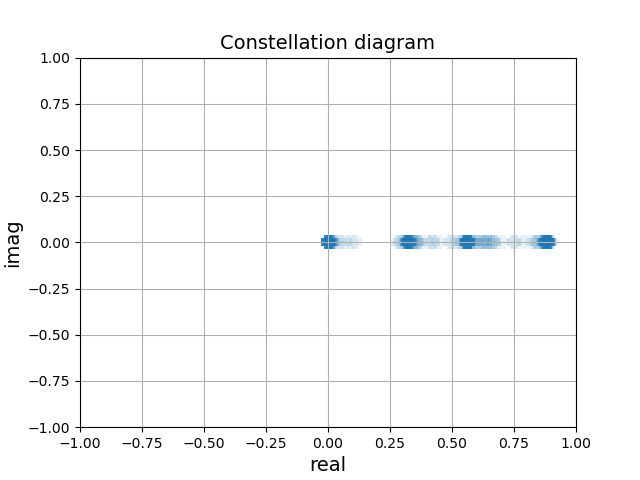
Finally, we plot the constellation diagram which is a graphical representation used in digital communications to visualize the complex-valued symbols transmitted over a communication channel. Each point in the diagram represents a symbol, which can be encoded as a combination of amplitude and phase.
# Plot Constellation diagram
########################################################################################################################
plt.figure(4)
res = result_modified_OOK(results)
plt.scatter(np.real(res), np.imag(res), marker="+", linewidths=10, alpha=0.1)
plt.grid()
plt.xlabel("real", fontsize=14)
plt.ylabel("imag", fontsize=14)
plt.title("Constellation diagram", fontsize=14)
plt.xlim([-1.0, 1.0])
plt.ylim([-1.0, 1.0])
plt.show()
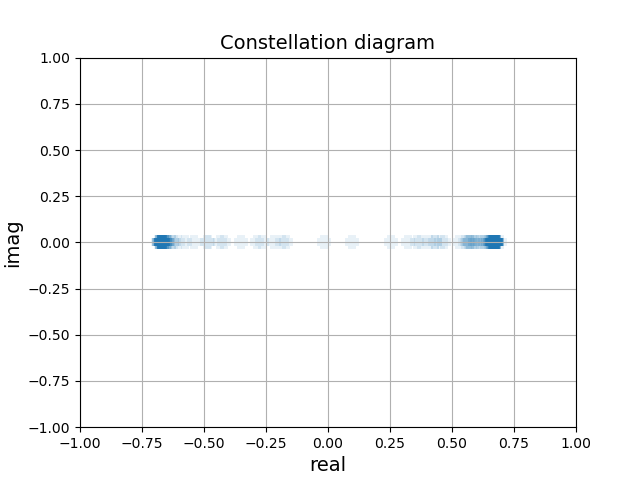
Binary Phase Shift Keying (BPSK)
BPSK is a digital modulation scheme where binary data (0s and 1s) is transmitted by shifting the phase of the carrier signal. In BPSK, one phase represents a binary “0” and the opposite phase represents a binary “1”. This modulation technique is widely used in communication systems due to its simplicity and resilience to noise. Typically, a logical “1” is represented by a phase shift of 180 degrees (or \(\pi\) radians), and a logical “0” is represented by no phase shift (0 degrees).
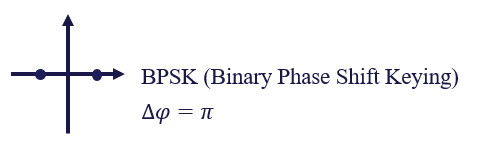
The example_mzm_BPSK_simulation.py file has the same format as the OOK example, however, this time we apply
V_pi to MZM1.
0 voltage to MZM2.
# Simulation of a MZM working in BPSK modulation format.
########################################################################################################################
results = simulate_modulation_mzm(
cell=mzm,
mod_amplitude=3.0,
mod_noise=0.5,
opt_amplitude=1.0,
opt_noise=0.01,
v_mzm1=V_half_pi, # MZM works at its Maximum transmission points
v_mzm2=0.0,
bit_rate=50e9,
n_bytes=2**8,
steps_per_bit=2**7,
center_wavelength=1.55,
The plotting of the eye diagram, constellation diagram and other results is the same.
Quadrature Phase Shift Keying (QPSK)
QPSK is a more advanced modulation scheme that is an extension of BPSK. So far we have considered modulation schemes that transmit one bit per symbol, however, QPSK is advantageous in terms of bandwidth efficiency as it transmits two bits per symbol.
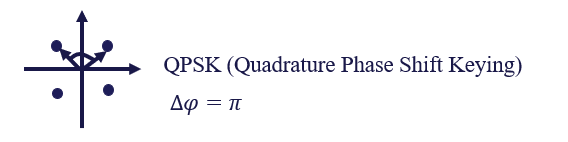
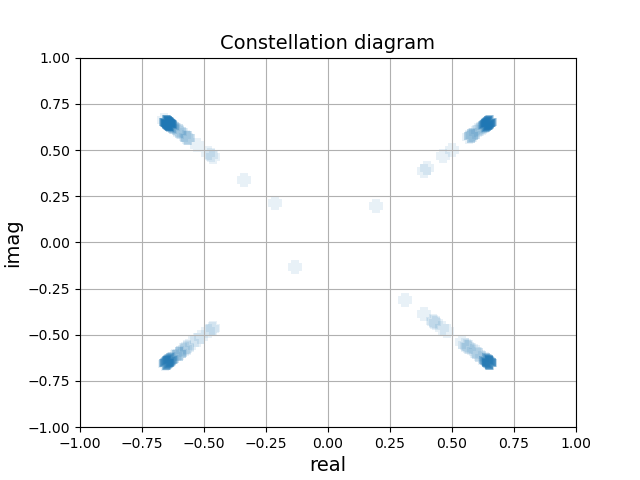
In QPSK, information is encoded in four phase states and two bits are required to identify a symbol. The four possible phase shifts in QPSK are: 0 degrees (00), 90 degrees (01), 180 degrees (10), and 270 degrees (11), or equivalently, 0, \(\pi/2\) , \(\pi\) , and \(3\pi/2\) radians.
The file example_iqmodulator_QPSK_simulation.py contains the same building blocks and all of the parameters we need to simulate QPSK by applying voltages to the IQ modulator and not the MZM.
# Simulation of a IQ modulator working in QPSK modulation format.
########################################################################################################################
results = simulate_modulation_iqmod(
cell=IQ_mod,
mod_amplitude_i=3.0,
mod_noise_i=0.5,
mod_amplitude_q=3.0,
mod_noise_q=0.5,
opt_amplitude=2.0,
opt_noise=0.01,
v_heater_i=V_half_pi, # The half pi phase shift implements orthogonal modulation
v_heater_q=0.0,
In the simulate_modulation_iqmod function we define the cell as Iq_mod and apply the following voltages.
V_half_pi to the In-phase (I) heater
V_pi to
v_mzm_left1andv_mzm_right10 voltage to Quadrature heater (Q),
v_mzm_left2andv_mzm_right2
Pulse-Amplitude Modulation 4 (PAM4)
PAM-4 is a digital modulation scheme that represents two bits per symbol by using four levels of pulse amplitude. Each pair of bits is mapped to one of four amplitude levels. The amplitude levels are typically symmetrically spaced around zero, allowing for easy detection at the receiver.
The mapping for PAM-4 is as follows:

“00” corresponds to the lowest amplitude level.
“01” corresponds to a mid-low amplitude level.
“10” corresponds to a mid-high amplitude level.
“11” corresponds to the highest amplitude level.
# Simulation of a IQ modulator working in PAM4 modulation format.
########################################################################################################################
results = simulate_modulation_iqmod(
cell=IQ_mod,
mod_amplitude_i=4.0,
mod_noise_i=0.1,
mod_amplitude_q=2.0,
mod_noise_q=0.1,
opt_amplitude=1.0,
opt_noise=0.01,
v_heater_i=0.0, # 4-Level Amplitude Modulation, thus no phase shift
v_heater_q=0.0,
In the simulate_modulation_iqmod function we define the cell as Iq_mod and apply the following voltages
V_half_pi to
v_mzm_left1andv_mzm_right1.0 voltage to the In-Phase (I) and Quadrature (Q) heaters.
0 voltage to
v_mzm_left2andv_mzm_right2.
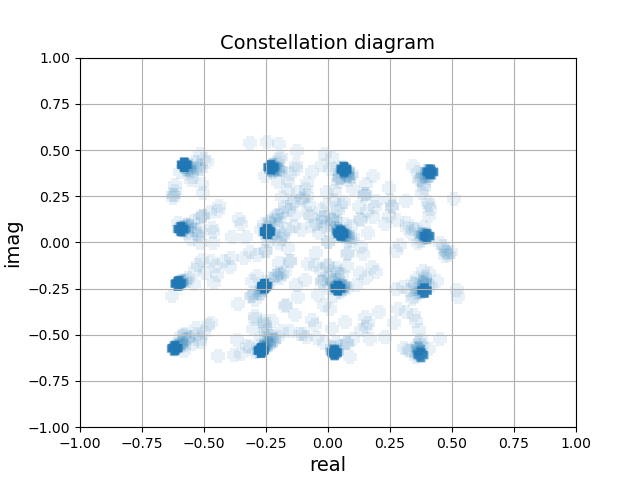
16-Quadrature Amplitude Modulation (16-QAM)
16-QAM is a digital modulation scheme that represents four bits per symbol by using combinations of both amplitude and phase shifts. Each group of four bits is mapped to one of sixteen possible combinations of amplitude and phase representing 0000, 0001, and so on.
# Simulation of a IQ modulator working in 16QAM modulation format.
########################################################################################################################
results = simulate_modulation_QAM(
cell=IQ_mod,
mod_amplitude_i=3.0,
mod_noise_i=0.1,
mod_amplitude_q=3.0,
mod_noise_q=0.1,
opt_amplitude=2.0,
opt_noise=0.01,
v_heater_i=V_half_pi, # The half pi phase shift implements orthogonal modulation
v_heater_q=0.0,
We apply the following voltages to the heaters and MZMs to drive the IQ modulator in the 16QAM modulation scheme.
V_half_pi to the In-phase (I) heater
V_pi to
v_mzm_left1andv_mzm_right10 voltage to Quadrature heater (Q),
v_mzm_left2andv_mzm_right2