Mach-Zehnder interferometer
The Mach-Zehnder interferometer (MZI) we are going to design is composed of:
One input fiber grating coupler
Two 2x1 MMIs
One output fiber grating coupler
Two waveguide arms (left and right) connecting the two inputs (used as outputs) of the first MMI to the two inputs of the second.
IPKISS integrates the different aspects of photonic design into one framework, where you can define your component once as a parametric cell (PCell) and then use it throughout the whole design process, allowing to tightly link layout and simulations.
Therefore, in order to easily create and manipulate the MZI that we need, we are going to create a PCell.
This PCell inherits from i3.Circuit, a class that makes it is easy to place and connect components together to achieve the final circuit.
PCell Properties
The first step is to define the PCell properties, which will be used to design the MZI. One aspect to pay attention to is the right arm of the MZI. Depending on the length of this arm, the result of the MZI simulation will change. Therefore, we need to be able to control the shape of this arm when we instantiate the MZI PCell, without touching the code inside the PCell itself.
The PCell has the following accessible properties:
control_point: This is a coordinate (control point) through which the right (longest) arm of the MZI has to pass. This allows us to control the shape of the right arm when we instantiate the MZI.bend_radius: Here, we assign the value of the bend radius to be used for the waveguide routes. In the CORNERSTONE SiN PDK, the minimum bend radius is 80 micron for the default waveguide width (1.2 micron) operating in C-band.fgc_spacing_y: This the separation in the y-dimension between the two fibre grating couplers.fgc: The PCell of the fiber grating coupler to be used. The default value isSiN300nm_1550nm_TE_STRIP_Grating_Couplerfrom the Luceda PDK for CORNERSTONE SiN.splitter: The PCell of the splitter to be used. The default value isStrip2x1MMIFixedfrom the library ‘pteam_library_conrerstone_sin’ which provides a circuit model for the classStrip2x1MMIin the Luceda PDK for CORNERSTONE SiN with a given set of parameters.
Below is the code that defines the PCell properties.
class MZI(i3.Circuit):
control_point = i3.Coord2Property(doc="Point that the longer arm of the MZI has to go through")
bend_radius = i3.PositiveNumberProperty(default=80.0, doc="Bend radius of the waveguides")
fgc_spacing_y = i3.PositiveNumberProperty(default=400.0, doc="Spacing of the fibre couplers")
fgc = i3.ChildCellProperty(doc="PCell for the fiber grating coupler")
splitter = i3.ChildCellProperty(doc="PCell for the splitter")
def _default_control_point(self):
return [(100.0, self.fgc_spacing_y / 2)]
def _default_fgc(self):
return pdk.SiN300nm_1550nm_TE_STRIP_Grating_Coupler()
def _default_splitter(self):
return Strip2x1MMIFixed()
Cells, placement and connections
The next step is to define a list of cells that will be instantiated. We need two fiber grating couplers and two splitters.
def _default_insts(self):
insts = {
"fgc_1": self.fgc,
"fgc_2": self.fgc,
"mmi_1": self.splitter,
"mmi_2": self.splitter,
}
return insts
We place the input port of the bottom fiber grating coupler at the origin (0.0, 0.0).
We then create an array of fiber grating couplers by placing the second grating coupler at a distance of fgc_spacing_y above the first.
def _default_specs(self):
br = self.bend_radius
ra = i3.SplineRoundingAlgorithm(adiabatic_angles=(15, 15))
specs = [
i3.Place("fgc_1:out", (-300, 0)),
i3.Join("fgc_1:out", "mmi_1:out"),
i3.Join("fgc_2:out", "mmi_2:out"),
i3.Place("fgc_2:out", (0.0, self.fgc_spacing_y), relative_to="fgc_1:out"),
i3.ConnectManhattan(
"mmi_1:in1",
"mmi_2:in2",
"mmi_1_in1_to_mmi_2_in2",
rounding_algorithm=ra,
bend_radius=br,
),
i3.ConnectManhattan(
"mmi_1:in2",
"mmi_2:in1",
"mmi_2_in2_to_mmi_1_in1",
rounding_algorithm=ra,
bend_radius=br,
control_points=[self.control_point],
),
]
return specs
The connections between the instances are defined differently depending on whether we connect them end-to-end or use a waveguide connector:
For end-to-end connections we use
i3.Join. Here, we use this for the connections between the input and output fiber grating couplers and the two splitters.To connect components using waveguide connectors, we use connectors (
i3.Connector). Here, we specify the type of connector used between the desired ports together with other useful information, such as the bend radius of the waveguides.
Components that are placed end-to-end using i3.Join are automatically placed by IPKISS to ensure that the connection requirement is satisfied.
In the case of connections defined using connectors, this is not the case.
IPKISS only knows that these two components have to be connected and the waveguide connector will be generated depending on their position, which we need to specify ourselves.
The connections between the two splitters (between “mmi1:in1” and “mmi2:in2”, and “mmi1:in2” and “mmi2:in1”) are performed using a Manhattan-type waveguide connector (i3.ConnectManhattan).
The right arm of the MMI (second connection) is forced to pass through the control point specified with the control_points coordinate when instantiating the PCell.
Exposed ports
Our circuit is almost finished. All we need to do now is to define the names of the external ports we want to access. We will use these port names to plot the transmission when we perform the circuit simulation.
def _default_exposed_ports(self):
exposed_ports = {
"fgc_1:vertical_in": "in",
"fgc_2:vertical_in": "out",
}
return exposed_ports
Run the code
Open luceda-academy/training/topical_training/cornerstone_mzi_sweep/mzi_pcell.py.
At the bottom of the file, the MZI is instantiated and simulated:
# Layout
mzi = MZI(
name="MZI",
control_point=(70.0, 200.0),
bend_radius=80.0,
)
mzi_layout = mzi.Layout()
mzi_layout.visualize()
mzi_layout.visualize_2d()
mzi_layout.write_gdsii("mzi.gds")
# Circuit model
my_circuit_cm = mzi.CircuitModel()
wavelengths = np.linspace(1.52, 1.58, 5001)
S_total = my_circuit_cm.get_smatrix(wavelengths=wavelengths)
# Plotting
S_total.visualize(
term_pairs=[
("in", "out"), # TE transmission
],
scale="dB",
yrange=(-100, 0),
)
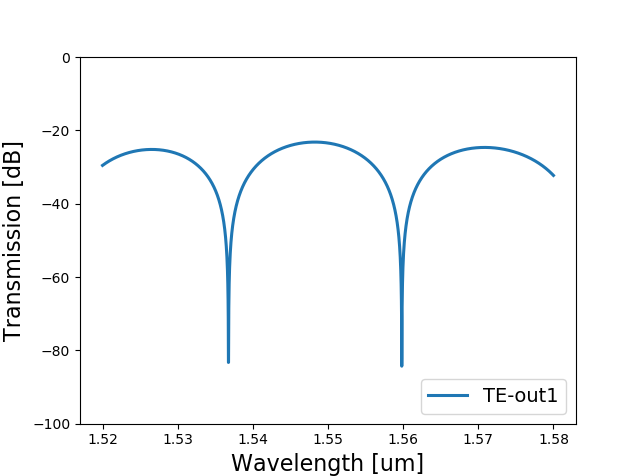
If you run the code, you will visualize the layout and the simulation of an MZI circuit for control_point=[(70.0, 200.0)] and bend_radius=80.0.
Test your knowledge
Try to change the coordinates of the control point and the bend radius to see how the simulation changes. What happens when the delay arm becomes longer? Why?