Basic Shapes
IPKISS shapes are all subclasses of the basic Shape class.
Basic shape |
|
Shape defined by a parametric function |
|
Basic circle |
|
Circular arc |
|
Circular arc specified by its starting point instead of its center |
|
Bend with relative turning angle instead of absolute end angle |
|
Cross. |
|
Wedge, or symmetric trapezium. |
|
Radial wedge: the coordinates of the start and end point are specified in polar coordinates from a given center |
|
Basic ellipse |
|
Ellipse arc around a given center. |
|
Basic rectangle |
|
Rectangle with rounded corners |
|
Ring segment |
|
Regular N-sided polygon |
|
Hexagon |
|
Dodecagon |
|
Parabolic wedge (taper) |
|
Exponential wedge (taper) |
|
Raised Sine S-bend |
|
Cosine S-bend |
|
Radial S-bend |
|
Cubic Hermite spline S-bend |
|
Euler spline S-bend |
|
Radial/Circular S-bend with minimized footprint in the x-dimension |
|
Euler spline S-bend with minimized footprint in the x-dimension |
|
Defines a coupler bend as S-bend-straight-S-bend. |
Shape
- class ipkiss3.all.Shape
Basic shape
- Parameters:
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 shape = i3.Shape(points=[(0.0, 0.0), (10.0, 10.0)]) print(shape.points) # returns the points of the shape # array([[ 0., 0.], # [ 10., 10.]]) print(len(shape)) # returns the number of points of the shape # 2 shape.get_face_angles() # returns (start_face_angle, end_face_angle), # (45.0, 45.0): these are the angles at the start and the end of an open shape. shape.closed # returns whether the shape is closed or not. # False: If you set closed=True, the shape will be filled. wg_layout = i3.Waveguide().Layout(shape=shape) wg_layout.visualize()
"""The start_face_angle is not equivalent to the waveguide port angle, as it points inwards and not outwards. The end_face_angle, however, is equivalent to the waveguide port angle.""" import ipkiss3.all as i3 shape = i3.Shape(points=[(0.0, 0.0), (10.0, 10.0)]) shape.start_face_angle = 10.0 wg_layout2 = i3.Waveguide().Layout(shape=shape) wg_layout2.visualize()
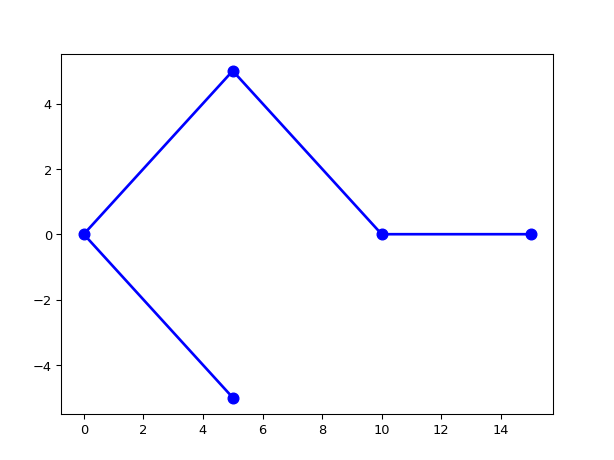
import ipkiss3.all as i3 s1 = i3.Shape([(5.0, -5.0), (0.0, 0.0), (5.0, 5.0), (10.0, 0.0)], closed=False) p2 = i3.Coord2((15.0, 0.0)) s2 = s1 + p2 s2.visualize()
ParametricShape
- class ipkiss3.all.ParametricShape
Shape defined by a parametric function
The shape is defined by a function curve(t) -> x(t), y(t) The normalized parameter t is a floating point value varied between 0.0 and t_max to generate the curve.
For instance, the equations x = cos(t) and y = sin(t) form the parametric equation of the unit circle. Sensible values for t depend on the equations. The property t_max can be set to choose the maximum t value the curve function is evaluated for.
A classical iterative midpoint sampling algorithm is used for calculating the shape. In each iteration, the list of t sample values is updated with the midpoints between each pair of t values, and is then evaluated to get the updated x,y coordinates.
Additional sample points will be added to the shape until adding a new sample point is deviating minimally from a straight line through its neighbours. The accuracy of the curve can be tweaked by choosing the maximum deviation (max_deviation property).
By default, the algorithm starts from the start and end of the curve, [0.0, t_max], as the sample points. Since for several shapes (e.g. a circle) this does not give the desired outcome, the initial sample points can be chosen by setting initial_t. This should be a monotonically increasing list starting with 0.0 and ending with t_max (or monotonically decreasing if t_max is negative).
The algorithm stops hard after max_refine_depth iterations even if the desired accuracy max_deviation is not reached yet, in order to avoid too deep iteration.
- Parameters:
- max_refine_depth: int, optional
maximum number of refinement iterations
- initial_t: list, optional
monotonically increasing list of initial values between 0 and t_max, for which the curve function is evaluated to bootstrap the curve.
- t_max: float, optional
maximum value of the parameter t, defaults to 1.0
- max_deviation: float, optional
maximum deviation of the discretized points from the analytical curve
- curve: optional
Parametric curve function curve(t) returning x and y for the given t
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
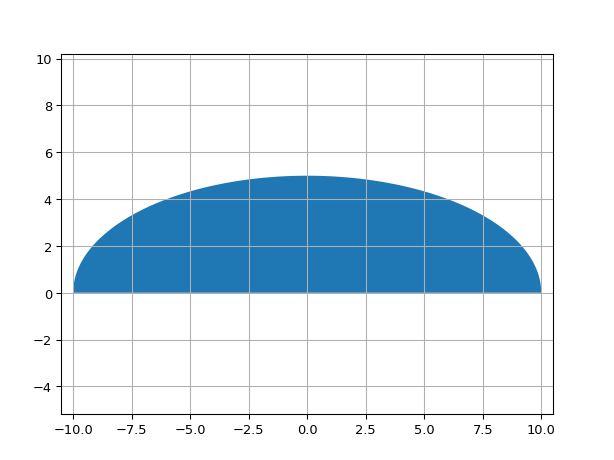
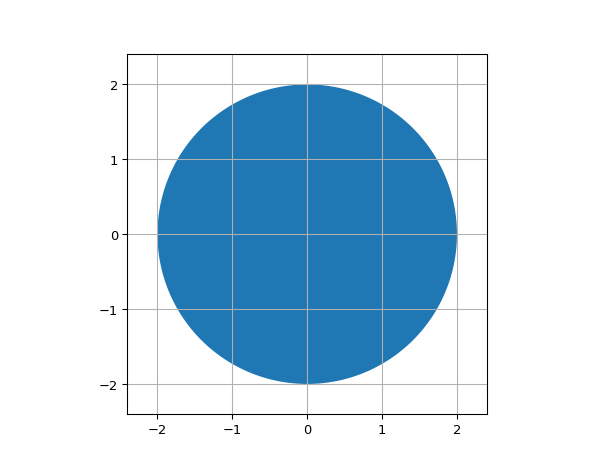
"""Half ellipse defined as parametric curve""" import ipkiss3.all as i3 import numpy as np # noqa def curve(t: float) -> tuple[float, float]: x = 10 * np.cos(t) y = 5 * np.sin(t) return x, y shape = i3.ParametricShape(curve=curve, initial_t=np.linspace(0, np.pi, 50).tolist(), t_max=np.pi) shape.close() shape.visualize()
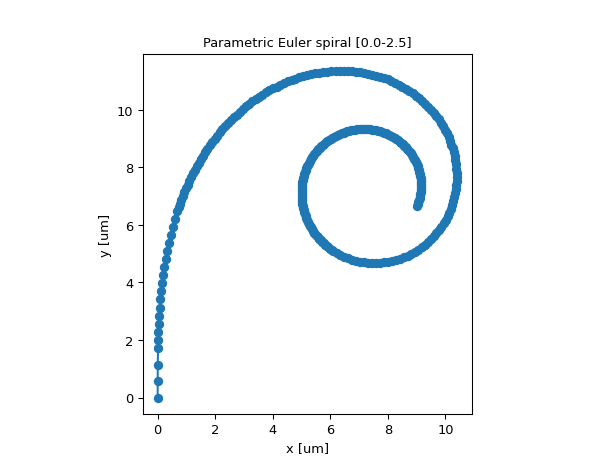
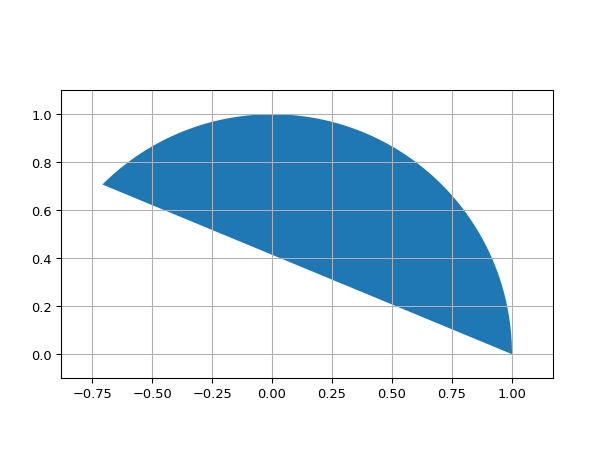
"""Euler spiral defined as parametric curve""" import ipkiss3.all as i3 from scipy.special import fresnel # fresnel(2) is the first full loop, calculate the scaling to have the first loop pass at a given x coordinate distance_x = 5.0 scaling = distance_x / fresnel(2)[0] def curve(t: float) -> tuple[float, float]: x, y = fresnel(t) return scaling * x, scaling * y shape = i3.ParametricShape(curve=curve, t_max=2.5) shape.visualize()
ShapeCircle
- class ipkiss3.all.ShapeCircle
Basic circle
- Parameters:
- radius: float and number > 0, optional
radius of the circular arc
- clockwise: optional
orientation of the arc. clockwise:True
- angle_step: float, optional
discretization angle
- end_angle: optional
- start_angle: optional
- box_size: optional
- center: Coord2, optional
center of the ellipse
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
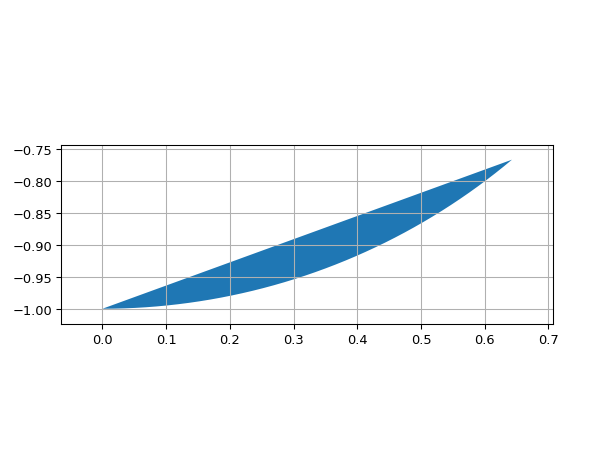
import ipkiss3.all as i3 i3.ShapeCircle(radius=2.0).visualize()
ShapeArc
- class ipkiss3.all.ShapeArc
Circular arc
- Parameters:
- radius: float and number > 0, optional
radius of the circular arc
- clockwise: optional
orientation of the arc. clockwise:True
- angle_step: float, optional
discretization angle
- end_angle: float, optional
end angle of the arc according to the parametric representation of an ellipse
- start_angle: float, optional
start angle of the arc according to the parametric representation of an ellipse
- box_size: optional
- center: Coord2, optional
center of the ellipse
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
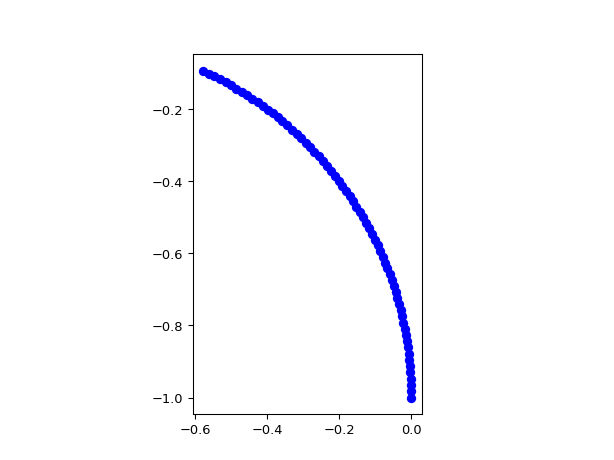
import ipkiss3.all as i3 i3.ShapeArc(start_angle=0, end_angle=90.0 + 45.0).visualize()
ShapeBend
- class ipkiss3.all.ShapeBend
Circular arc specified by its starting point instead of its center
- Parameters:
- output_angle: float, optional
- input_angle: float, optional
- start_point: Coord2, optional
starting point of the circular bend
- radius: float and number > 0, optional
radius of the circular arc
- clockwise: optional
orientation of the arc. clockwise:True
- angle_step: float, optional
discretization angle
- end_angle: optional
end angle in degrees
- start_angle: optional
start angle in degrees
- box_size: optional
- center: optional
center of the bend
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeBend(start_point=(0.0, -1.0), start_angle=270.0, end_angle=310.0).visualize()
ShapeBendRelative
- ipkiss3.all.ShapeBendRelative(start_point=(0.0, 0.0), radius=1.0, input_angle=0.0, angle_amount=90.0, angle_step=<ipkiss3.technology.TechValue object>, **kwargs)
Bend with relative turning angle instead of absolute end angle
- Parameters:
- start_pointtuple, optional
starting point of the circular bend
- radiusfloat, optional
radius of the circular arc
- input_anglefloat, optional
input angle in degrees
- angle_amountfloat, optional
angle amount in degrees
- angle_step: float, optional
angle step discretization in degrees
- **kwargs
same as ShapeBend
- Returns:
- ShapeBend class
Examples
import ipkiss3.all as i3
import matplotlib.pyplot as plt
# You can set the start_point to move the bend shapes, such as ShapeBend, ShapeBendRelative and S-bend Shapes.
shape = i3.ShapeBendRelative(start_point=(0.0, -1.0), input_angle=90.0, angle_amount=65.0)
shape.visualize()
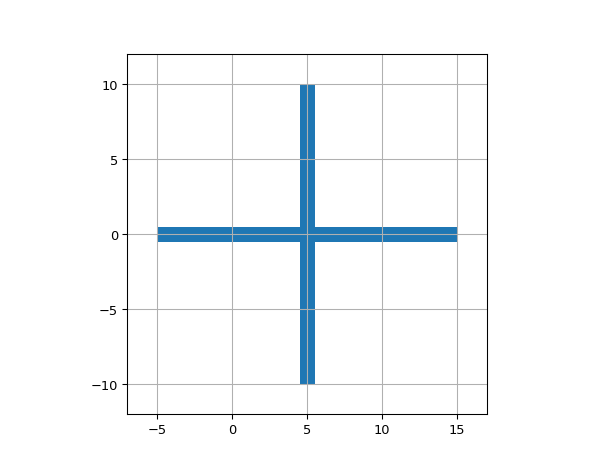
ShapeCross
- class ipkiss3.all.ShapeCross
Cross. Thickness sets the width of the arms
- Parameters:
- thickness: float and number > 0, optional
- box_size: float and number > 0, optional
- center: Coord2, optional
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeCross(center=(5.0, 0.0), thickness=1.0).visualize()
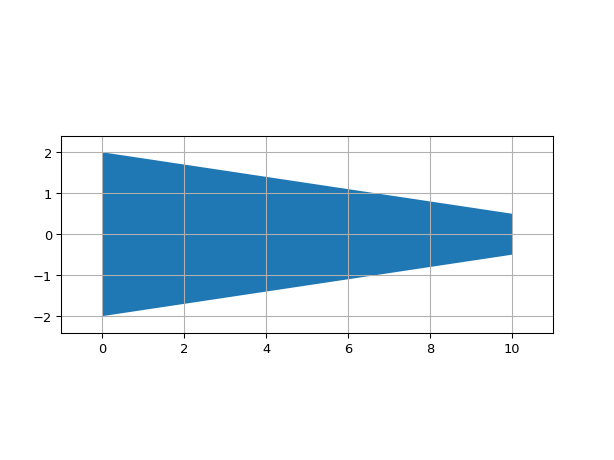
ShapeWedge
- class ipkiss3.all.ShapeWedge
Wedge, or symmetric trapezium. Specified by the center of baselines and the length of the baselines
- Parameters:
- end_width: float and int, float, integer, floating and number >= 0, optional
- begin_width: float and int, float, integer, floating and number >= 0, optional
- end_coord: Coord2, optional
- begin_coord: Coord2, optional
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeWedge(begin_coord=(0.0, 0.0), end_coord=(10.0, 0.0), begin_width=4.0, end_width=1.0).visualize()
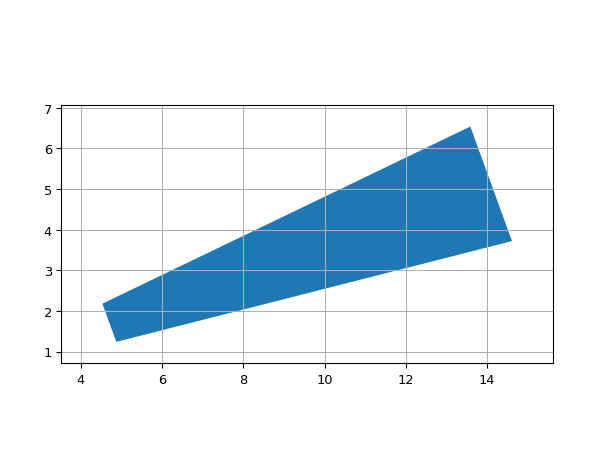
ShapeRadialWedge
- class ipkiss3.all.ShapeRadialWedge
Radial wedge: the coordinates of the start and end point are specified in polar coordinates from a given center
- Parameters:
- angle: float, required
- outer_width: float and number > 0, required
- inner_width: float and number > 0, required
- outer_radius: float and number > 0, required
- inner_radius: float and number > 0, required
- center: Coord2, optional
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeRadialWedge( inner_radius=5.0, outer_radius=15.0, inner_width=1.0, outer_width=3.0, angle=20.0 ).visualize()
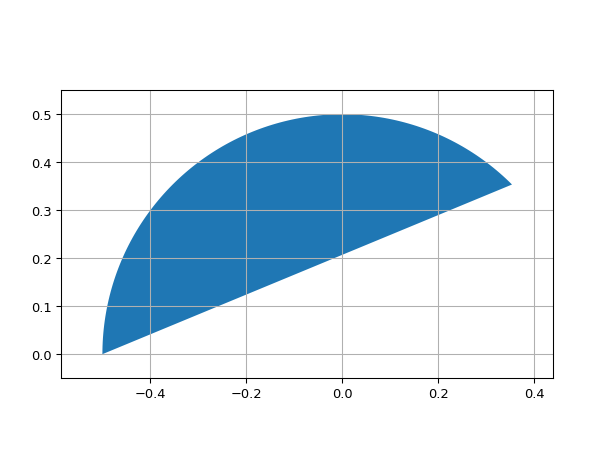
ShapeEllipse
- class ipkiss3.all.ShapeEllipse
Basic ellipse
- Parameters:
- clockwise: optional
orientation of the arc. clockwise:True
- angle_step: float, optional
discretization angle
- end_angle: optional
- start_angle: optional
- box_size: Coord2 and number >= 0, optional
size of the ellipse along major and minor axis
- center: Coord2, optional
center of the ellipse
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeEllipse(start_angle=45.0, end_angle=180.0).visualize()
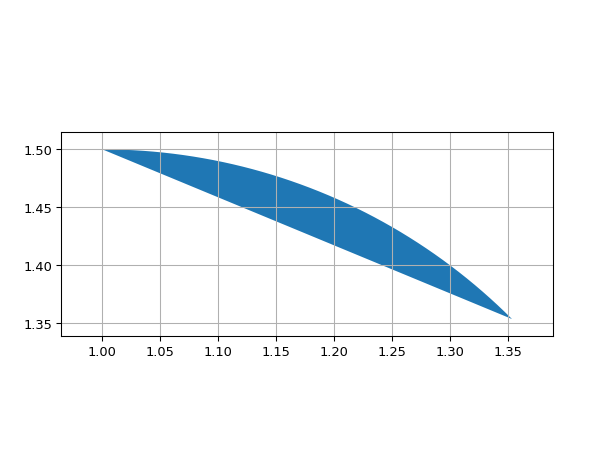
ShapeEllipseArc
- class ipkiss3.all.ShapeEllipseArc
Ellipse arc around a given center.
ShapeEllipseArc implements the standard parametric representation of an ellipse (x = a * cos(t), y = b * sin(t)) and (0 <= t < 2 * pi), where parameter t is not the actual angle, but has a geometric meaning due to Philippe de La Hire.
The start_angle and end_angle are described as this parameter t.
- Parameters:
- clockwise: optional
orientation of the arc. clockwise:True
- angle_step: float, optional
discretization angle
- end_angle: float, optional
end angle of the arc according to the parametric representation of an ellipse
- start_angle: float, optional
start angle of the arc according to the parametric representation of an ellipse
- box_size: Coord2 and number >= 0, optional
size of the ellipse along major and minor axis
- center: Coord2, optional
center of the ellipse
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Notes
If you want to get the parametric angle t from the actual angle alpha, you can use the following:
import numpy as np a, b = box_size t = np.arctan2(2. / b * np.sin(alpha), 2. / a * np.cos(alpha)) # t and alpha in radians
Examples
import ipkiss3.all as i3 i3.ShapeEllipseArc(start_angle=45.0, center=(1.0, 1.0)).visualize()
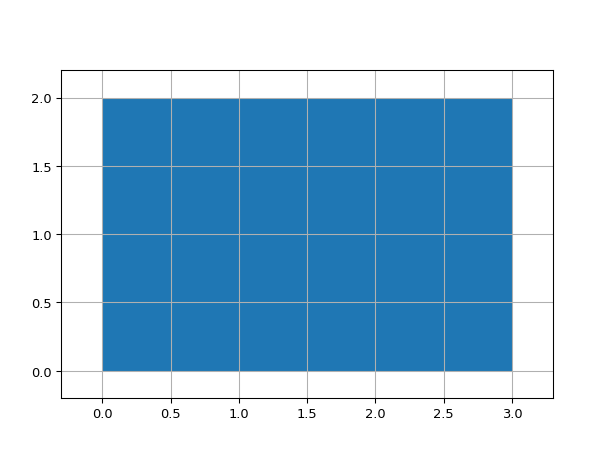
ShapeRectangle
- class ipkiss3.all.ShapeRectangle
Basic rectangle
- Parameters:
- angle_step: float, optional
angle_step using in the rounding.
- radius: optional
- box_size: Coord2 and number >= 0, optional
size of the rectangle.
- center: Coord2, optional
center of the rectangle.
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeRectangle(center=(1.5, 1.0), box_size=(3.0, 2.0)).visualize()
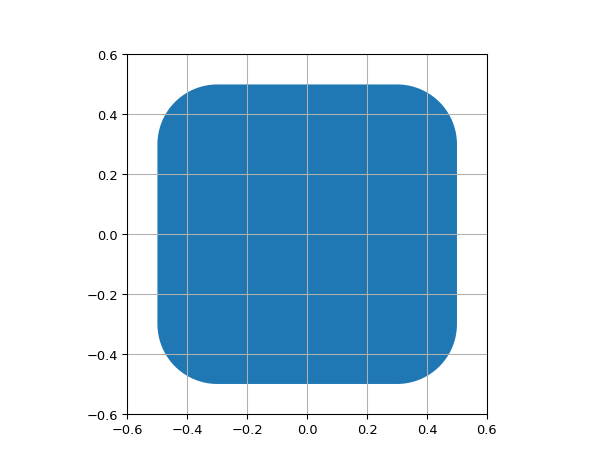
ShapeRoundedRectangle
- class ipkiss3.all.ShapeRoundedRectangle
Rectangle with rounded corners
- Parameters:
- angle_step: float, optional
angle_step using in the rounding.
- radius: float and int, float, integer, floating and number >= 0, optional
radius of the rounding used.
- box_size: Coord2 and number >= 0, optional
size of the rectangle.
- center: Coord2, optional
center of the rectangle.
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeRoundedRectangle(center=(0.0, 0.0), box_size=(1.0, 1.0), radius=0.2).visualize()
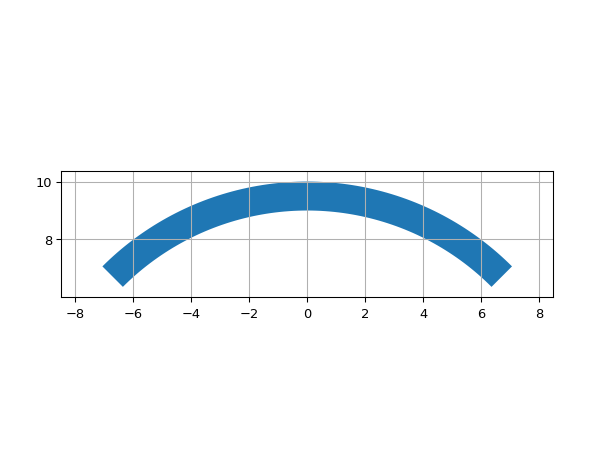
ShapeRingSegment
- class ipkiss3.all.ShapeRingSegment
Ring segment
- Parameters:
- outer_radius: float and number > 0, required
- inner_radius: float and number > 0, required
- angle_step: float, optional
- angle_end: float, optional
- angle_start: float, optional
- center: Coord2, optional
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeRingSegment( center=(0.0, 0.0), angle_start=45.0, angle_end=45.0 + 90.0, inner_radius=9.0, outer_radius=10.0 ).visualize()
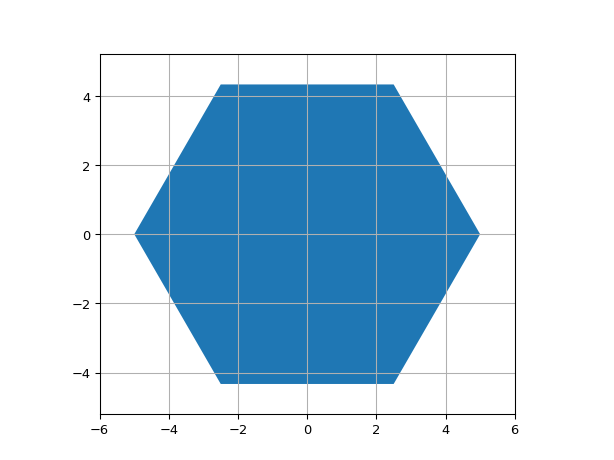
ShapeHexagon
- class ipkiss3.all.ShapeHexagon
Hexagon
- Parameters:
- radius: float and number > 0, optional
Radius of the polygon
- center: Coord2, optional
Center of the polygon
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- n_o_sides: int and [3,None], locked
Number of sides of the hexagon
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeHexagon(center=(0.0, 0.0), radius=5.0).visualize()
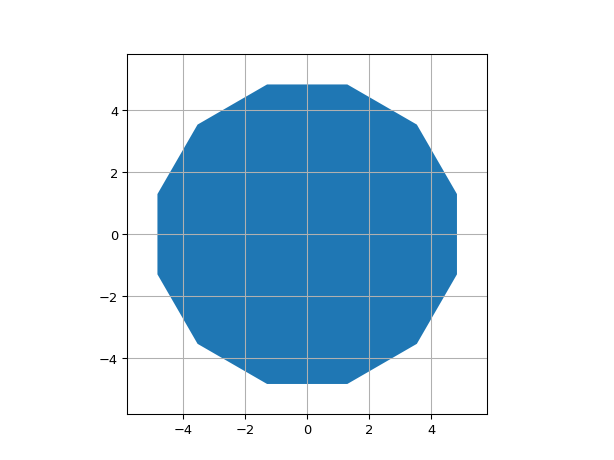
ShapeDodecagon
- class ipkiss3.all.ShapeDodecagon
Dodecagon
- Parameters:
- n_o_sides: int and [3,None], optional
- radius: float and number > 0, optional
Radius of the polygon
- center: Coord2, optional
Center of the polygon
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeDodecagon(center=(0.0, 0.0), radius=5.0).visualize()
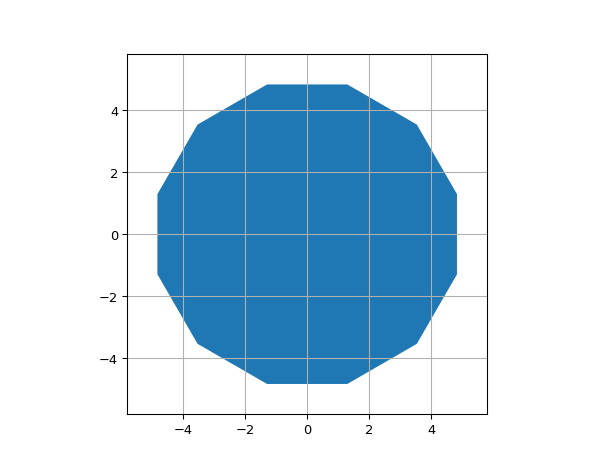
ShapeRegularPolygon
- class ipkiss3.all.ShapeRegularPolygon
Regular N-sided polygon
- Parameters:
- n_o_sides: int and [3,None], optional
Number of sides fo the polygon
- radius: float and number > 0, optional
Radius of the polygon
- center: Coord2, optional
Center of the polygon
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeRegularPolygon(center=(0.0, 0.0), n_o_sides=12, radius=5.0).visualize()
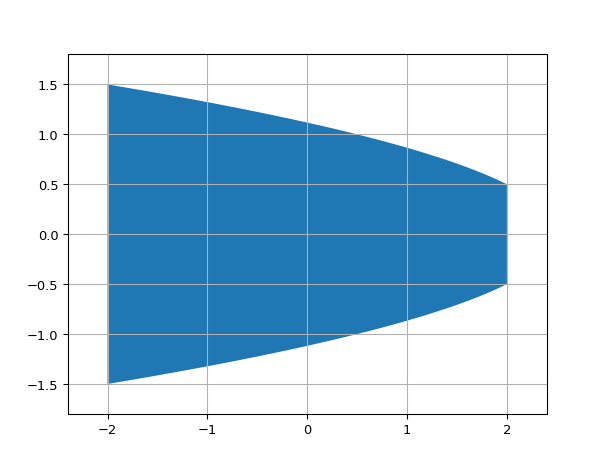
ShapeParabolic
- class ipkiss3.all.ShapeParabolic
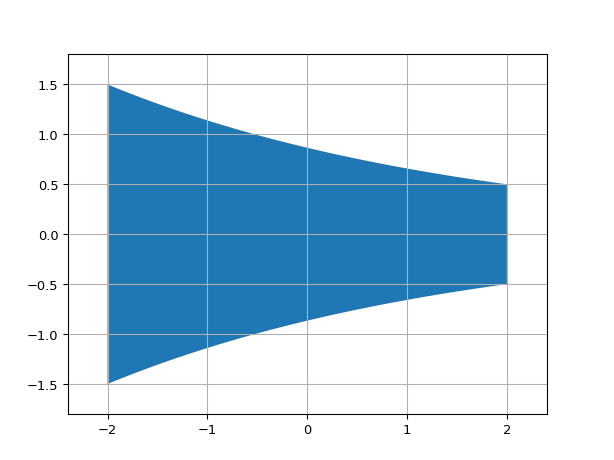
Parabolic wedge (taper)
- Parameters:
- width_step: float and number > 0, optional
maximum width step in discretized shape. Defaults to 10.0 * TECH.METRICS.GRID / TECH.METRICS.UNIT.
- end_width: float and int, float, integer, floating and number >= 0, optional
- begin_width: float and int, float, integer, floating and number >= 0, optional
- end_coord: Coord2, optional
- begin_coord: Coord2, optional
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeParabolic(begin_coord=(-2.0, 0.0), end_coord=(2.0, 0.0), begin_width=3.0, end_width=1.0).visualize()
ShapeExponential
- class ipkiss3.all.ShapeExponential
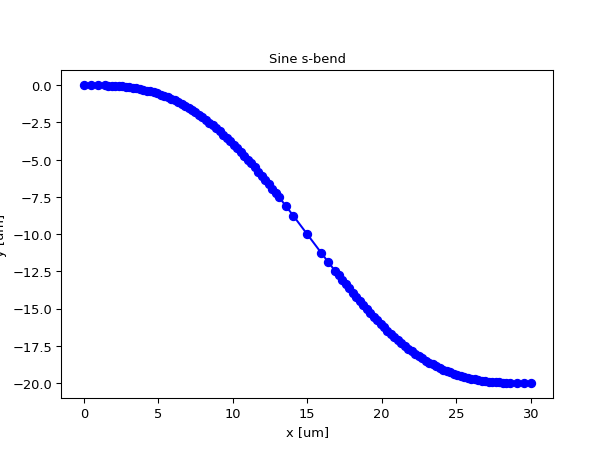
Exponential wedge (taper)
- Parameters:
- g: float and int, float, integer, floating and number >= 0, optional
Exponential growth constant. Defaults to ln(max_width/min_width)
- width_step: float and number > 0, optional
maximum width step in discretized shape. Defaults to 10.0 * TECH.METRICS.GRID / TECH.METRICS.UNIT.
- end_width: float and int, float, integer, floating and number >= 0, optional
- begin_width: float and int, float, integer, floating and number >= 0, optional
- end_coord: Coord2, optional
- begin_coord: Coord2, optional
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeExponential(begin_coord=(-2.0, 0.0), end_coord=(2.0, 0.0), begin_width=3.0, end_width=1.0).visualize()
S-bend Shapes
- class ipkiss3.all.ShapeSineSBend
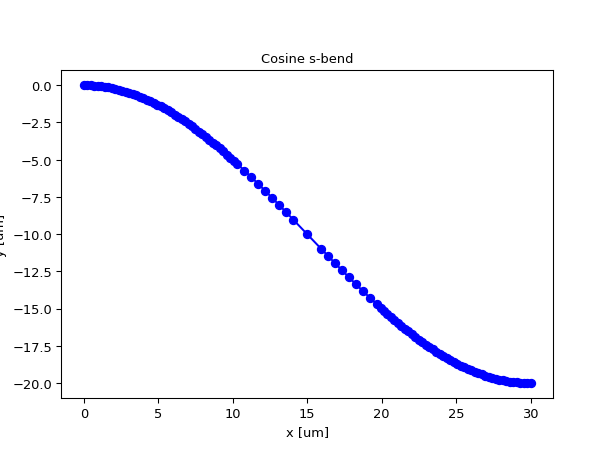
Raised Sine S-bend
- Parameters:
- y_offset: float, required
transversal offset the bend makes.
- x_offset: float, required
offset in x covered by the bend.
- max_refine_depth: int, optional
maximum number of refinement iterations
- initial_t: list, optional
monotonically increasing list of initial values between 0 and t_max, for which the curve function is evaluated to bootstrap the curve.
- max_deviation: float, optional
maximum deviation of the discretized points from the analytical curve
- start_angle: float, optional
start angle of the bend
- start_point: Coord2, optional
start point of the bend
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeSineSBend(x_offset=30.0, y_offset=-20.0).visualize()
- class ipkiss3.all.ShapeCosineSBend
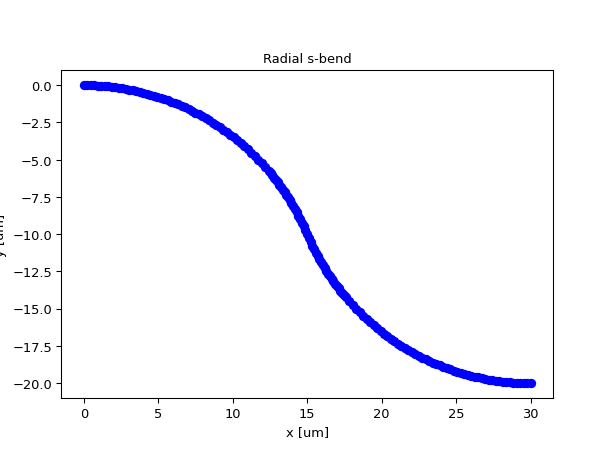
Cosine S-bend
- Parameters:
- y_offset: float, required
transversal offset the bend makes.
- x_offset: float, required
offset in x covered by the bend.
- max_refine_depth: int, optional
maximum number of refinement iterations
- initial_t: list, optional
monotonically increasing list of initial values between 0 and t_max, for which the curve function is evaluated to bootstrap the curve.
- max_deviation: float, optional
maximum deviation of the discretized points from the analytical curve
- start_angle: float, optional
start angle of the bend
- start_point: Coord2, optional
start point of the bend
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeCosineSBend(x_offset=30.0, y_offset=-20.0).visualize()
- class ipkiss3.all.ShapeRadialSBend
Radial S-bend
- Parameters:
- y_offset: float, required
transversal offset the bend makes.
- x_offset: float, required
offset in x covered by the bend.
- max_refine_depth: int, optional
maximum number of refinement iterations
- initial_t: list, optional
monotonically increasing list of initial values between 0 and t_max, for which the curve function is evaluated to bootstrap the curve.
- max_deviation: float, optional
maximum deviation of the discretized points from the analytical curve
- start_angle: float, optional
start angle of the bend
- start_point: Coord2, optional
start point of the bend
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
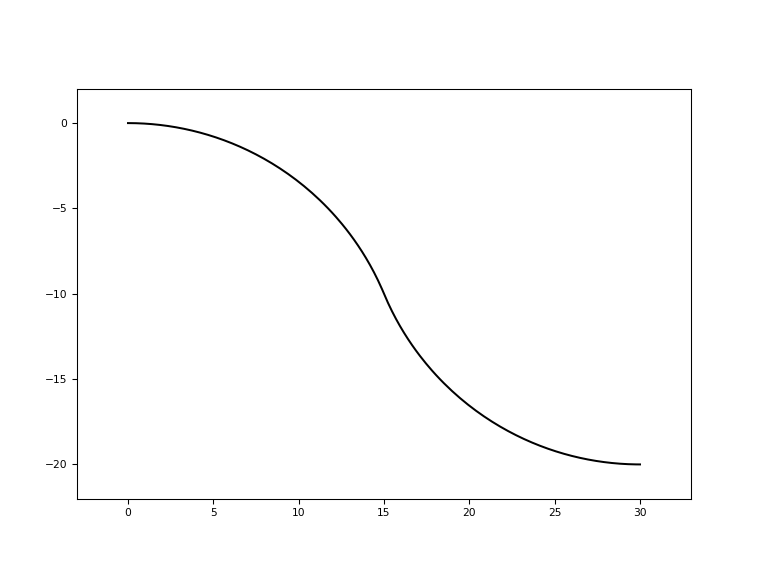
import ipkiss3.all as i3 i3.ShapeRadialSBend(x_offset=30.0, y_offset=-20.0).visualize()
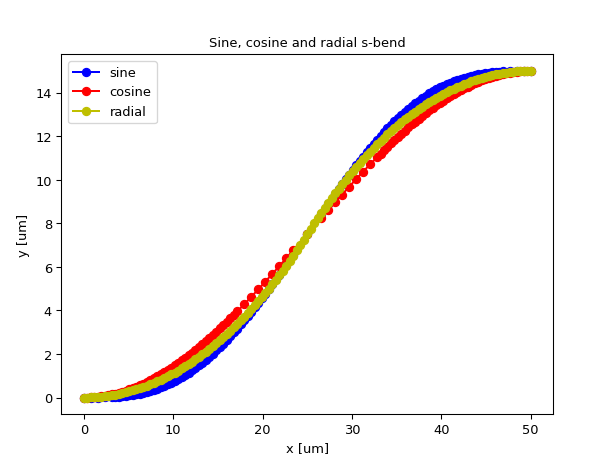
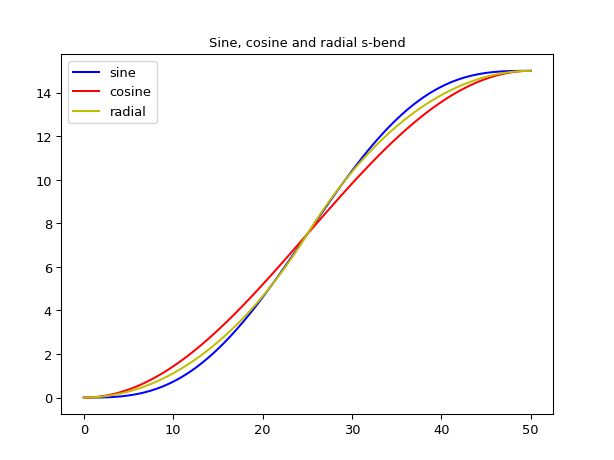
Examples
import ipkiss3.all as i3
import matplotlib.pyplot as plt
L = 50.0
H = 15.0
sh_sine = i3.ShapeSineSBend(x_offset=L, y_offset=H)
sh_cosine = i3.ShapeCosineSBend(x_offset=L, y_offset=H)
sh_radial = i3.ShapeRadialSBend(x_offset=L, y_offset=H)
plt.plot(sh_sine.x_coords(), sh_sine.y_coords(), 'b-', label='sine')
plt.plot(sh_cosine.x_coords(), sh_cosine.y_coords(), 'r-', label='cosine')
plt.plot(sh_radial.x_coords(), sh_radial.y_coords(), 'y-', label='radial')
plt.legend()
plt.title('Sine, cosine and radial s-bend')
plt.show()
- class ipkiss3.all.ShapeHermiteSBend
Cubic Hermite spline S-bend
- Parameters:
- y_offset: float, required
transversal offset the bend makes.
- x_offset: float, required
offset in x covered by the bend.
- m: float, optional
tangent size for the start and end point (see https://en.wikipedia.org/wiki/Cubic_Hermite_spline), if not specified, m will be chosen such that it has the maximal bend radii. This is the vector size pointed to the center .
- max_refine_depth: int, optional
maximum number of refinement iterations
- initial_t: list, optional
monotonically increasing list of initial values between 0 and t_max, for which the curve function is evaluated to bootstrap the curve.
- max_deviation: float, optional
maximum deviation of the discretized points from the analytical curve
- start_angle: float, optional
start angle of the bend
- start_point: Coord2, optional
start point of the bend
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
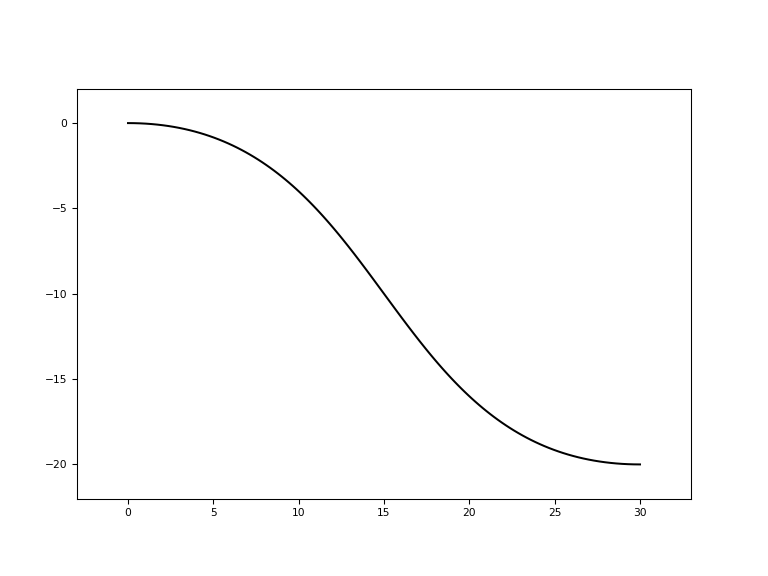
import ipkiss3.all as i3 i3.ShapeHermiteSBend(x_offset=30.0, y_offset=-20.0).visualize()
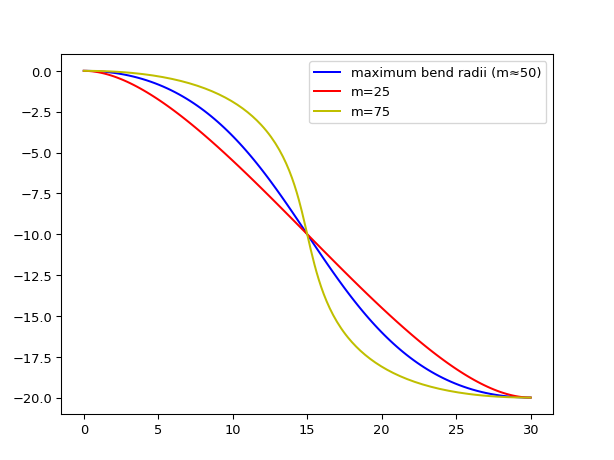
import ipkiss3.all as i3 import matplotlib.pyplot as plt L = 30.0 H = -20.0 shm = i3.ShapeHermiteSBend(x_offset=L, y_offset=H) sh25 = i3.ShapeHermiteSBend(x_offset=L, y_offset=H, m=25) sh75 = i3.ShapeHermiteSBend(x_offset=L, y_offset=H, m=75) plt.plot(shm.x_coords(), shm.y_coords(), "b-", label="maximum bend radii (m≈50)") plt.plot(sh25.x_coords(), sh25.y_coords(), "r-", label="m=25") plt.plot(sh75.x_coords(), sh75.y_coords(), "y-", label="m=75") plt.legend() plt.show()
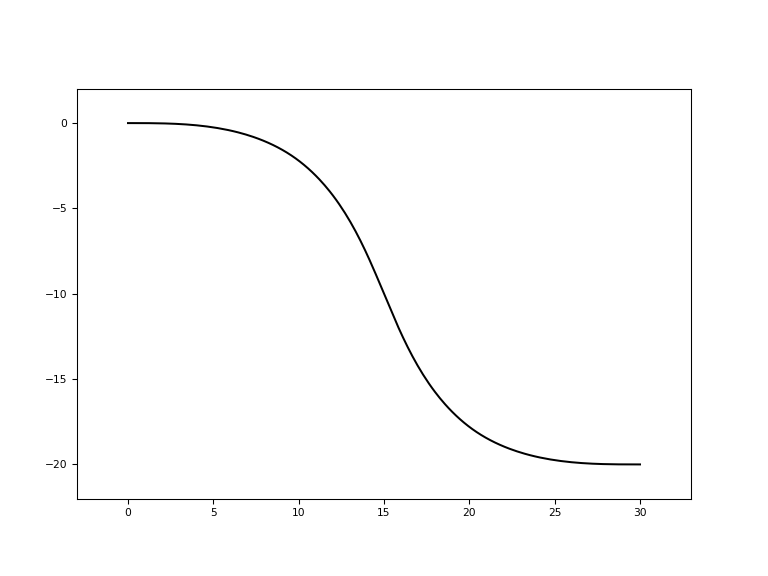
- class ipkiss3.all.ShapeEulerSBend
Euler spline S-bend
This is created by joining 4 euler bends together for a certain angle (arctan(y_offset/x_offset), and then fitting this to the right point.
Since there is the middle of the S-bend angle is double of the total angle, and there is a relation between the end angle of an euler, there exist only 1 solution to fit 4 symmetrical euler bends in the area x_offset and y_offset.
Note that this is a pure Euler bend, and thus keeps linearly increasing it 1/R until 1/4 or 3/4 of the curve. Thus, there is no minimal bend radii to be set, but this can be found by 1/(np.sqrt(self.phi / np.pi)*self.a).
- Parameters:
- y_offset: float, required
transversal offset the bend makes.
- x_offset: float, required
offset in x covered by the bend.
- max_refine_depth: int, optional
maximum number of refinement iterations
- initial_t: list, optional
monotonically increasing list of initial values between 0 and t_max, for which the curve function is evaluated to bootstrap the curve.
- max_deviation: float, optional
maximum deviation of the discretized points from the analytical curve
- start_angle: float, optional
start angle of the bend
- start_point: Coord2, optional
start point of the bend
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- a: float, locked
The scaling factor of the euler curve.
- phi: float, locked
The join angle at the center of the curve. In radials.
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeEulerSBend(x_offset=30.0, y_offset=-20.0).visualize()
- class ipkiss3.all.ShapeMinimizedRadialSBend
Radial/Circular S-bend with minimized footprint in the x-dimension
This shape creates a radial/circular S-bend with a specified radius, ensuring the y-offset matches the specified value while minimizing the footprint in the x-dimension.
- Parameters:
- y_offset: float, required
transversal offset the bend makes.
- radius: float and number > 0, optional
Radius of the radial/circular bend.
- max_refine_depth: int, optional
maximum number of refinement iterations
- initial_t: list, optional
monotonically increasing list of initial values between 0 and t_max, for which the curve function is evaluated to bootstrap the curve.
- max_deviation: float, optional
maximum deviation of the discretized points from the analytical curve
- start_angle: float, optional
start angle of the bend
- start_point: Coord2, optional
start point of the bend
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- t_max: float, locked
- phi: float, locked
Join angle at the center of the curve (in radians).
- x_offset: float, locked
Horizontal offset covered by the bend.
- size_info: SizeInfo, locked
get the size information on this Shape
Examples
import ipkiss3.all as i3 i3.ShapeMinimizedRadialSBend(y_offset=20, radius=5).visualize()
- class ipkiss3.all.ShapeMinimizedEulerSBend
Euler spline S-bend with minimized footprint in the x-dimension
This shapes creates a Euler S-bend with a specified minimum radius, ensuring the y-offset matches the specified value while minimizing the footprint in the x-dimension.
- Parameters:
- y_offset: float, required
transversal offset the bend makes.
- min_radius: float and number > 0, optional
Minimum radius of the Euler bend.
- max_refine_depth: int, optional
maximum number of refinement iterations
- initial_t: list, optional
monotonically increasing list of initial values between 0 and t_max, for which the curve function is evaluated to bootstrap the curve.
- max_deviation: float, optional
maximum deviation of the discretized points from the analytical curve
- start_angle: float, optional
start angle of the bend
- start_point: Coord2, optional
start point of the bend
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- phi: float, locked
Join angle at the center of the curve (in degrees).
- t_max: float, locked
- x_offset: float, locked
Horizontal offset covered by the bend.
- size_info: SizeInfo, locked
get the size information on this Shape
Notes
Accuracy. As generating an Euler S-bend with the smallest footprint, given the minimum radius and y-offset is computationally intensive, this class offers a computationally efficient solution with a minimal deviation from the smallest possible Euler S-bend.
Differences between ShapeMinimizedEulerSBend and ShapeEulerSBend. The key difference between
ShapeMinimizedEulerSBendandShapeEulerSBendlies in how they handle the radius and offsets.ShapeMinimizedEulerSBendcreates a bend with a specified minimum radius, ensuring the y-offset matches the specified value while minimizing the x-offset. On the other hand,ShapeEulerSBenddoes not offer control over the minimum radius and instead creates a shape based on the specified x- and y- offsets.Examples
# The result is an S bend starting at (0,0) with a height of 20, minimum bend radius of 4 # and the shortest possible distance in the x direction import ipkiss3.all as i3 i3.ShapeMinimizedEulerSBend(y_offset=20, min_radius=5).visualize()
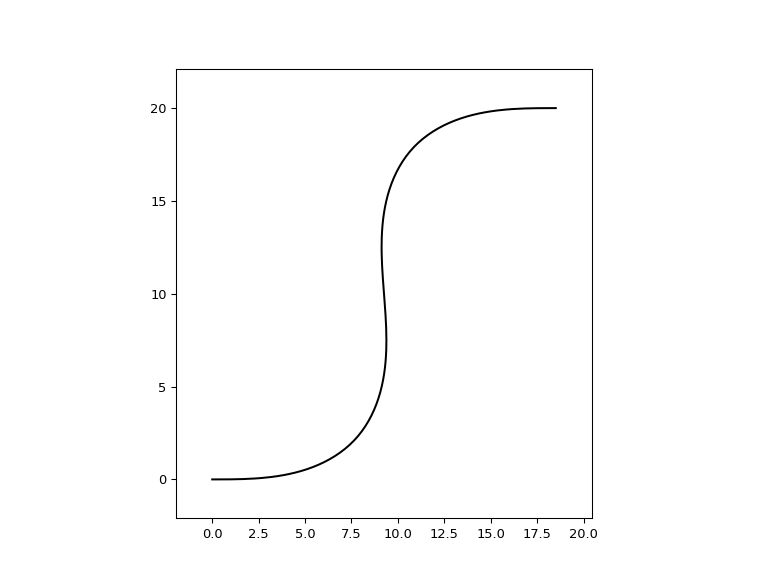
Coupler shapes
- class ipkiss3.all.ShapeCoupler
Defines a coupler bend as S-bend-straight-S-bend.
- Parameters:
- y_offset: float, required
transversal offset the bends makes.
- x_offset: float, required
offset in x covered by the bends.
- straight_length: float and number > 0, required
length of the straight portion between the S-bends.
- sbend: str and String that contains only ISO/IEC 8859-1 (extended ASCII py3) or pure ASCII (py2) characters and List with value restriction, allowed values: (‘sin’, ‘cos’, ‘rad’, ‘hermite’, ‘euler’), optional
Defines which S-bend will be used.Options are ‘sin’ for Raised Sine S-bend, ‘cos’ for Cosine S-bend, ‘rad’ for Radial S-bend, ‘hermite’ for Hermite S-bend and ‘euler’ for Euler S-bend.
- closed: optional
is the shape closed or not
- end_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the end of an open shape
- start_face_angle: ( float ), optional, *None allowed*
Use this to overrule the ‘dangling’ angle at the start of an open shape
- points: optional
points of this shape
- Other Parameters:
- sbenddict: OrderedTypedDict, locked
- size_info: SizeInfo, locked
get the size information on this Shape
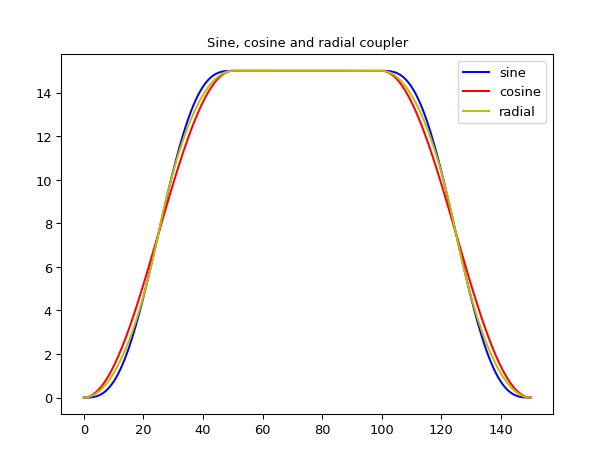
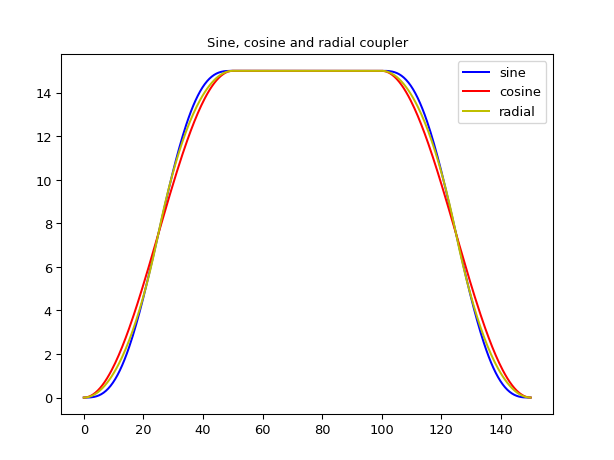
Examples
import ipkiss3.all as i3 import matplotlib.pyplot as plt L = 50.0 H = 15.0 sh_sine = i3.ShapeCoupler(straight_length=50, sbend="sin", x_offset=L, y_offset=H) sh_cosine = i3.ShapeCoupler(straight_length=50, sbend="cos", x_offset=L, y_offset=H) sh_radial = i3.ShapeCoupler(straight_length=50, sbend="rad", x_offset=L, y_offset=H) plt.plot(sh_sine.x_coords(), sh_sine.y_coords(), "b-", label="sine") plt.plot(sh_cosine.x_coords(), sh_cosine.y_coords(), "r-", label="cosine") plt.plot(sh_radial.x_coords(), sh_radial.y_coords(), "y-", label="radial") plt.legend() plt.title("Sine, cosine and radial coupler") plt.show()