DC3

class ipkiss3.cml.DC3

General length-dependent directional coupler model based on kappa and kappa_0.

This model is dispersive and can also account for incomplete coupling for larger coupling lengths.

Parameters:

k_a: float

First asymmetry factor to describe the incomplete coupling

k_b: float

Second asymmetry factor to describe the incomplete coupling

kappa: List[float] (/μm)

Length dependent field coupling in the straight section, as a polynomial of wavelength (μm), centered around center_wavelength. Highest order coefficient first.

kappa_0: List[float]

Field coupling in the bend sections, as a polynomial of wavelength (μm), centered around center_wavelength. Highest order coefficient first.

insertion_loss: float (dB)

Insertion loss in decibels.

center_wavelength: float (μm)

Center wavelength of the cross coupling.

coupler_length: float (μm)

Length of the directional coupler.

phase_bar: list[float] (rad)

Phase delay to bar port, as a polynomial of wavelength (μm), centered around center_wavelength. Highest order coefficient first.

phase_cross: list[float] (rad)

Phase delay to cross port, as a polynomial of wavelength (μm), centered around center_wavelength. Highest order coefficient first.

Notes

The coupled power (excluding insertion loss) is given by:

\[K_c(\lambda, L) = K_a + K_b \sin^2\left(\kappa^{\prime}(\lambda)L + \kappa_0(\lambda)\right)\]

Here, \(K_a\) and \(K_b\) (e.g., \(K_b = 1 - 2K_a\)) define the asymmetry of the WGs at the outer edges (incomplete coupling), while \(\kappa^{\prime}(\lambda)\) and \(\kappa_0(\lambda)\) are the wavelength-dependent coupling coefficients.

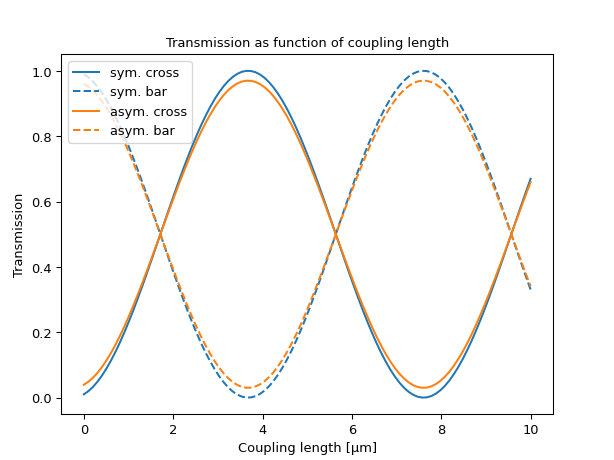
The incomplete coupling causes deviations from the ideal sinusoidal power transfer, leading to altered coupling behavior and, in some cases, increased coupling strength. The effect is typically minor and becomes noticeable only for larger coupler lengths.

In addition, the user can specify the insertion loss (dB) and the phase delay (rad) at both the bar and cross ports. A constant phase difference of \(\pi/2\) is typically set between the two ports, which is appropriate only for lossless, symmetrical directional couplers.

Terms

Term Name	Type	#modes
in1	Optical	1
in2	Optical	1
out1	Optical	1
out2	Optical	1

Examples

import numpy as np
import ipkiss3.all as i3
import matplotlib.pyplot as plt

lengths = np.linspace(0, 10, 100)
cross_sym, bar_sym, cross_asym, bar_asym = [np.zeros_like(lengths) for _ in range(4)]

for ndx, length in enumerate(lengths):
    k_a = 0.03
    k_b = 1 - 2 * k_a

    kappa, kappa_0 = [-0.5, 0.4], [0.3, 0.1]

    center_wavelength, n_avg, L_total = 1.3, 2.7, 20
    phase_l_avg = (
        2 * np.pi / center_wavelength * n_avg * L_total
    )  # Average phase delay from input to output port (dispersionless)
    phase_bar = [0, phase_l_avg]  # Phase for bar port
    phase_cross = [0, phase_l_avg + np.pi / 2]  # 90° phase difference between bar and cross ports

    model_sym = i3.cml.DC3(
        k_a=0.0,
        k_b=1.0,
        kappa=kappa,
        kappa_0=kappa_0,
        center_wavelength=center_wavelength,
        insertion_loss=0.0,
        coupler_length=length,
        phase_bar=phase_bar,
        phase_cross=phase_cross,
    )
    model_asym = i3.cml.DC3(
        k_a=k_a,
        k_b=k_b,
        kappa=kappa,
        kappa_0=kappa_0,
        center_wavelength=center_wavelength,
        insertion_loss=0.0,
        coupler_length=length,
        phase_bar=phase_bar,
        phase_cross=phase_cross,
    )

    S1 = i3.circuit_sim.test_circuitmodel(model_sym, [1.3])
    S2 = i3.circuit_sim.test_circuitmodel(model_asym, [1.3])

    cross_sym[ndx] = np.abs(S1["out2", "in1"][0]) ** 2
    bar_sym[ndx] = np.abs(S1["out1", "in1"][0]) ** 2
    cross_asym[ndx] = np.abs(S2["out2", "in1"][0]) ** 2
    bar_asym[ndx] = np.abs(S2["out1", "in1"][0]) ** 2

plt.figure()
plt.plot(lengths, cross_sym, "-", label="sym. cross", color="tab:blue")
plt.plot(lengths, bar_sym, "--", label="sym. bar", color="tab:blue")
plt.plot(lengths, cross_asym, "-", label="asym. cross", color="tab:orange")
plt.plot(lengths, bar_asym, "--", label="asym. bar", color="tab:orange")
plt.xlabel("Coupling length [μm]")
plt.ylabel("Transmission")
plt.title("Transmission as function of coupling length")
plt.legend()
plt.show()