WG2
- class ipkiss3.cml.WG2
Single mode polynomial waveguide model.
Uses a polynomial expression of the effective index and loss (in dB/m) as function of wavelength offset.
- Parameters:
- n_eff: List[float]
Polynomial coefficients of the mode effective index as function of wavelength offset from center_wavelength [/m^n]. Highest order first (effective index at center_wavelength last).
- loss: List[float]
Polynomial coefficients of the loss of the waveguide mode as function of wavelength offset from center_wavelength [dB/m / m^n]. Highest order first (loss at center_wavelength last).
- center_wavelength: float (m)
Center wavelength (in meter) of the model around which n_eff and loss are defined.
- length: float (m)
Total length of the waveguide in meter.
Notes
The effective index and loss are calculated as:
\[ \begin{align}\begin{aligned}n_{eff}(\lambda) = n_{eff}[n] + (\lambda-\lambda_c) * n_{eff}[n-1] + ... + (\lambda-\lambda_c)^2 * n_{eff}[0]\\loss(\lambda) = loss[n] + (\lambda-\lambda_c) * loss[n-1] + ... + (\lambda-\lambda_c)^2 * loss[0]\end{aligned}\end{align} \]Where n is the order of the polynomial, \(\lambda_c\) is the central wavelength at which \(n_{eff}(\lambda_c) == n_{eff}[n]\) and \($loss(\lambda_c) = loss[n]\).
The scatter matrix is given by:
\[\begin{split}\mathbf{S}_{wg}=\begin{bmatrix} 0 & \exp(-j\frac{2 \pi}{\lambda}L n_{eff}(\lambda)) * A \\ \exp(-j\frac{2 \pi}{\lambda}L n_{eff}(\lambda)) * A & 0 \end{bmatrix}\end{split}\]Where the amplitude loss is calculated as:
\[A = 10^{-loss * L * 1e-4 / 20.0}\]Terms
Term Name
Type
#modes
in
Optical
1
out
Optical
1
Examples
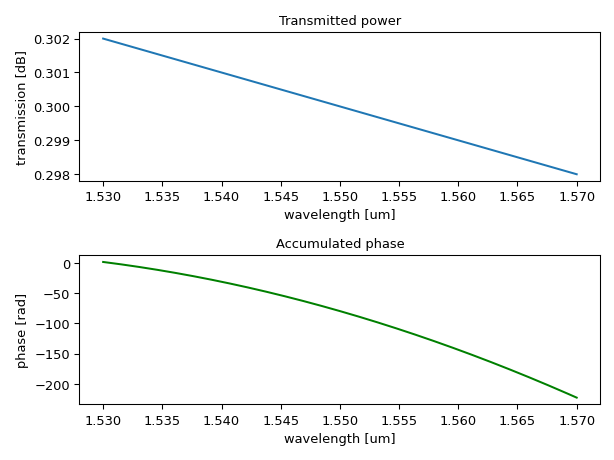
import numpy as np import ipkiss3.all as i3 import matplotlib.pyplot as plt # test model model = i3.cml.WG2( n_eff=[-20.0, -0.1, 2.0], loss=[1.0 * 100.0, -3.0 * 100.0], center_wavelength=1.55e-6, length=1000.0 * 1e-6, ) wavelengths = np.linspace(1.53, 1.57, 2001) S = i3.circuit_sim.test_circuitmodel(model, wavelengths) # plot loss and phase transmission = 10 * np.log10(np.abs(S["out", "in"]) ** 2) phase = np.unwrap(np.angle(S["out", "in"])) plt.subplot(211) plt.plot(wavelengths, transmission) plt.xlabel("wavelength [um]") plt.ylabel("transmission [dB]") plt.title("Transmitted power") plt.subplot(212) plt.plot(wavelengths, phase, "g-") plt.xlabel("wavelength [um]") plt.ylabel("phase [rad]") plt.title("Accumulated phase") plt.tight_layout() plt.show()
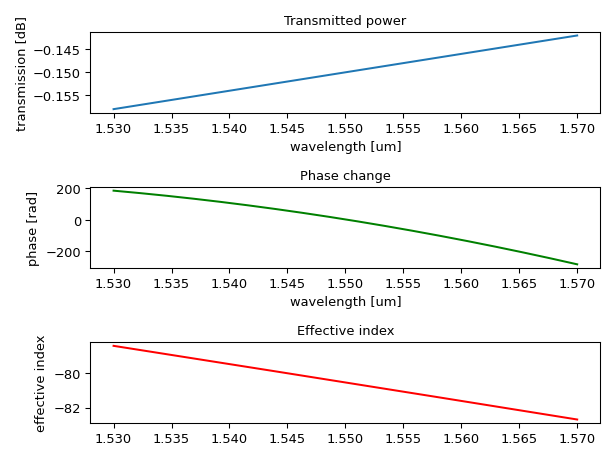
import numpy as np import ipkiss3.all as i3 import matplotlib.pyplot as plt # waveguide data effective_index = 2.4 group_index = 4.5 # use a high GVD to simulate a long waveguide while avoiding large phase jumps group_velocity_dispersion = 580 * 300 * 1e-12 / (1e-9 * 1e3) # s /(m * m) center_wavelength = 1.55e-6 # m c = 299792458.0 # m /s length = 1000.0 * 1e-6 # m # model parameters dneff_dlambda = (effective_index - group_index) / center_wavelength * 1e-6 # /m dneff2_dlambda2 = -group_velocity_dispersion * c / center_wavelength * 1e-12 # [/m^2] n_eff_coefficients = [dneff2_dlambda2, dneff_dlambda, effective_index] loss_coefficients = [-4.0 * 100.0, 1.5 * 100.0] # test model model = i3.cml.WG2( n_eff=n_eff_coefficients, loss=loss_coefficients, center_wavelength=center_wavelength, length=length, ) wavelengths = np.linspace(1.53, 1.57, 2001) S = i3.circuit_sim.test_circuitmodel(model, wavelengths) # plot loss, phase and effective index transmission = 10 * np.log10(np.abs(S["out", "in"]) ** 2) # unwrap the phase relative to the center wavelength center_index = np.where(wavelengths == 1.55)[0][0] phase = np.angle(S["out", "in"]) unwrapped_phase = np.concatenate( (np.unwrap(phase[0:center_index][::-1])[::-1], np.unwrap(phase[center_index:])) ) # calculate neff ourselves - wavelength relative to center_wavelength neff = np.polyval(n_eff_coefficients, wavelengths - center_wavelength) plt.subplot(311) plt.plot(wavelengths, transmission) plt.xlabel("wavelength [um]") plt.ylabel("transmission [dB]") plt.title("Transmitted power") plt.subplot(312) plt.plot(wavelengths, unwrapped_phase, "g-") plt.xlabel("wavelength [um]") plt.ylabel("phase [rad]") plt.title("Phase change") plt.subplot(313) plt.plot(wavelengths, neff, "r-") plt.ylabel("effective index") plt.title("Effective index") plt.tight_layout() plt.show()