Release notes IPKISS 3.1.1

IPKISS 3.1.1 comes with a series of small improvements and bugfixes. A detailed list can be found in the changelog.

Highlights are shown below:

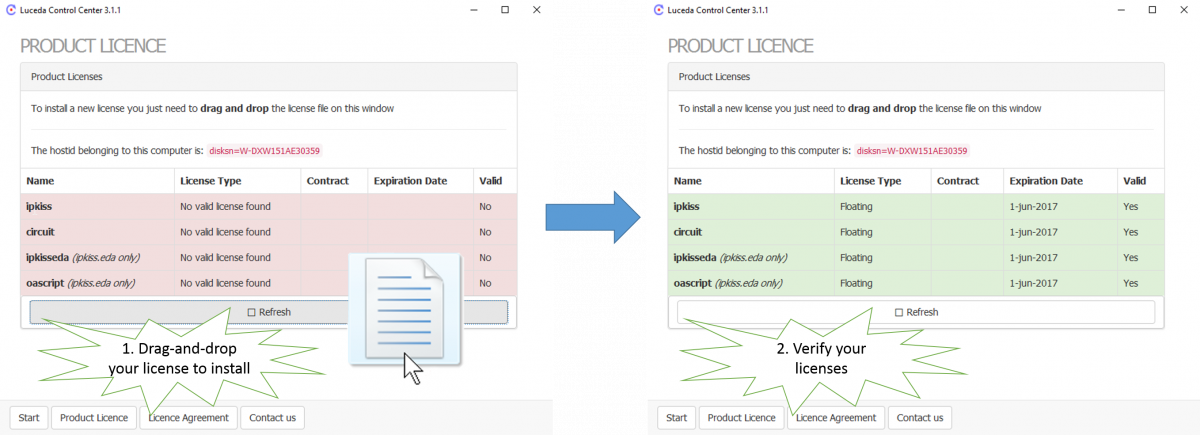
License installation and verification 

Installing licenses is now much simpler. In addition, you can verify whether your licenses have been installed properly. After installing, simply open the “Luceda Control Center” and go to the “Product License” tab. To install a license, drag-and-drop your license file into this tab. The table will show which licenses you have, and until when they are valid:

Product license panel in Luceda Control Center

Updated packages 

We have updated many packages in our Luceda distribution. Most notably, we now use conda 4, and include numpy (v1.11.2) and scipy (v0.18.1).

Visualization: ports can be labeled 

The visualize() method of a Layout view can show the ports by using visualize(annotate=True).

import si_fab.all as pdk
from ipkiss3 import all as i3
from picazzo3.filters.ring import RingRect180DropFilter

ring = RingRect180DropFilter()
ring_layout = ring.Layout(bend_radius=8.0)
ring_layout.visualize(annotate=True)

../_images/whatsnew_311_ports_visualization.png

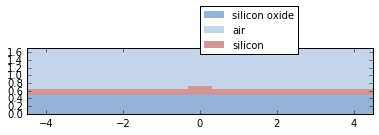
Cross-sections of trace templates 

Trace templates can now generate and visualize a cross-section geometry. Use cross_section() to get the cross-section, and visualize() to visualize.

import si_fab.all as pdk
from picazzo3.traces.rib_wg import RibWaveguideTemplate
rwg = RibWaveguideTemplate()
rwg_layout = rwg.Layout(core_width=.60)
rwg_layout.cross_section().visualize()

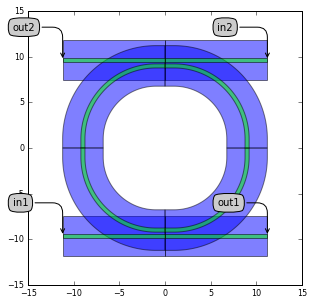
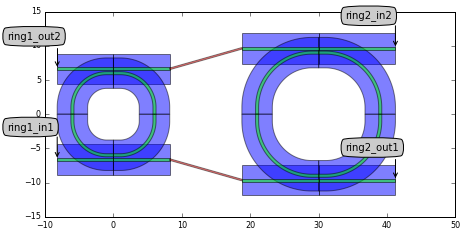
PlaceAndConnect draws flylines when links are not properly connected 

Flylines visually show when you haven’t properly connected components with PlaceAndConnect. The Layout view has two new parameters to control the behavior of the flylines:

flyline_layer (default: i3.TECH.PPLAYER.ERROR.GENERIC)
flyline_width (default: 0.5 * i3.TECH.WG.WIRE_WIDTH).

from picazzo3.routing.place_route import PlaceAndConnect
ring1 = RingRect180DropFilter()
ring2 = RingRect180DropFilter()
ring2.Layout(bend_radius=8.0)
pac = PlaceAndConnect(child_cells={'ring1': ring1, 'ring2': ring2},
                      links=[('ring1:out1', 'ring2:in1'), ('ring1:in2', 'ring2:out2')])
pac_lay = pac.Layout(child_transformations={'ring1': (0, 0), 'ring2': (30, 0)})
pac_lay.visualize(annotate=True)

Shapes for performing spline fitting 

Ipkiss now contains 2 new spline shapes:

ShapeFitNaturalCubicSpline ShapeFitClampedCubicSpline

See also the documentation here: spline shapes.

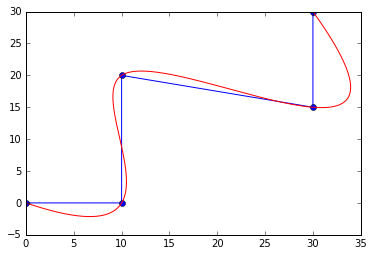
ShapeFitNaturalCubicSpline 

A natural cubic spline shape.

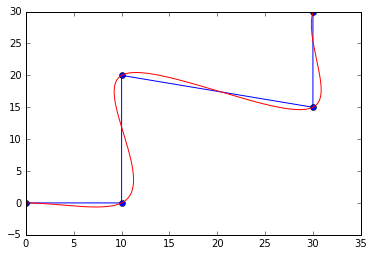
s = i3.Shape([(0.0, 0.0), (10.0, 0.0), (10.0, 20.0), (30.0, 15.0), (30.0, 30.0)])
s2 = i3.ShapeFitNaturalCubicSpline(original_shape=s, discretisation=.1)

# plot control shape
x, y = s.points.transpose()
plt.plot(x, y, 'bo-')
# plot spline
x2, y2 = s2.points.transpose()
plt.plot(x2, y2, 'r-')

ShapeFitClampedCubicSpline 

A cubic spline shape which can be clamped at the start / end to a fixed angle.

s = i3.Shape([(0.0, 0.0), (10.0, 0.0), (10.0, 20.0), (30.0, 15.0), (30.0, 30.0)],
             start_face_angle=0.0, end_face_angle=80.0)
s2 = i3.ShapeFitClampedCubicSpline(original_shape=s, discretisation=.1)

# plot control shape
x, y = s.points.transpose()
plt.plot(x, y, 'bo-')
# plot spline
x2, y2 = s2.points.transpose()
plt.plot(x2, y2, 'r-')