Advanced examples
Simulating a heated waveguide
Our circuit simulator ‘Caphe’ can also handle time-domain simulations. While the details are not within the scope of a getting started training, this example already gives an introduction. The first couple of steps should look familiar as the general format of the compact model is still the same.
Create a new compact model
class HeaterBroadBandPhaseErrorCompactModel(i3.CompactModel):
Add parameters.
parameters = [
"n_effs",
"loss_db_per_cm",
"wavelengths",
"length",
"width",
"phase_error",
"p_pi_sq",
"delta_lambda",
"v_bias_dc",
]
3. Add terms. We also add two electrical terms to apply a voltage difference across the waveguide.
terms = [
i3.OpticalTerm(name="in"),
i3.OpticalTerm(name="out"),
i3.ElectricalTerm(name="elec1"),
i3.ElectricalTerm(name="elec2"),
]
Implement the S-matrix
def calculate_smatrix(parameters, env, S):
# 2. This is the usual frequency domain S-matrix response for the component. It features a phase and loss
# calculation, hence enabling a complex expression for the transmission. There is no reflection in this model.
neff_total = np.interp(env.wavelength, parameters.wavelengths, np.real(parameters.n_effs)) + 1j * np.interp(
env.wavelength, parameters.wavelengths, np.imag(parameters.n_effs)
)
ratio = parameters.length / parameters.width
phase_mod = np.pi * (parameters.v_bias_dc**2) / (parameters.p_pi_sq * ratio)
beta = 2 * np.pi / env.wavelength * neff_total
loss = 10.0 ** (-(parameters.loss_db_per_cm * 1e-4 * parameters.length) / 20.0)
tot_phase = beta * parameters.length + parameters.phase_error * np.sqrt(parameters.length) + phase_mod
S["in", "out"] = S["out", "in"] = loss * np.exp(1j * tot_phase)
The main difference is that two new methods are available:
calculate_signals: Captures the time dependence of the output signal on the input signal. In this case we take the length and group velocity of the waveguide into account to calculate a time delay.calculate_dydt: Includes differential equations that describe the state of the system (e.g. temperature). This part is ommitted in this example.
def calculate_signals(parameters, env, output_signals, y, t, input_signals):
# 3. This function defines the output_signals as function of time (t), states (y), and the input_signals.
# The main difference is that the output signal is delayed using the length of the waveguide and the group
# velocity of the heated waveguide.
v_diff = abs(input_signals["elec2"] - input_signals["elec1"])
neff_total = np.interp(env.wavelength, parameters.wavelengths, np.real(parameters.n_effs)) + 1j * np.interp(
env.wavelength, parameters.wavelengths, np.imag(parameters.n_effs)
)
beta = 2 * np.pi / env.wavelength * neff_total
ratio = parameters.length / parameters.width
phase_mod = np.pi * (v_diff**2) / (parameters.p_pi_sq * ratio)
tot_phase = beta * parameters.length + parameters.phase_error * np.sqrt(parameters.length) + phase_mod
loss = 10.0 ** (-(parameters.loss_db_per_cm * 1e-4 * parameters.length) / 20.0)
transmission = loss * np.exp(1j * tot_phase)
neff_minus = np.interp(
env.wavelength - parameters.delta_lambda, parameters.wavelengths, np.real(parameters.n_effs)
)
neff_plus = np.interp(
env.wavelength + parameters.delta_lambda, parameters.wavelengths, np.real(parameters.n_effs)
)
dneff_dlambda = (neff_plus - neff_minus) / (2 * parameters.delta_lambda)
ng = np.real(neff_total) - env.wavelength * dneff_dlambda
t_delay = ng * parameters.length / (speed_of_light * 1e6)
output_signals["in"] = transmission * input_signals["out", t - t_delay]
output_signals["out"] = transmission * input_signals["in", t - t_delay]
As usual, this model can be attached to a PCell through its circuit model view.
class CircuitModel(i3.CircuitModelView):
# 7. We will assign parameters with a sensible default value directly (for the purposes of testing), whilst
# other values (the wavelength range and matching effective indices) can be derived directly from the trace
# template.
p_pi_sq = i3.PositiveNumberProperty(default=100e-3)
v_bias_dc = i3.NumberProperty(default=0.0)
delta_lambda = i3.PositiveNumberProperty(default=0.001)
loss_db_per_cm = i3.PositiveNumberProperty(default=2)
def _generate_model(self):
template = self.trace_template
wavelengths = template.wavelengths
neffs = np.array([template.get_n_eff(i3.Environment(wavelength=wl)) for wl in wavelengths])
return HeaterBroadBandPhaseErrorCompactModel( # return our model with completed parameters
length=100.0,
width=1.0,
n_effs=neffs,
loss_db_per_cm=self.loss_db_per_cm,
wavelengths=wavelengths,
phase_error=self.trace_template.get_phase_error(),
p_pi_sq=self.p_pi_sq,
delta_lambda=self.delta_lambda,
v_bias_dc=self.v_bias_dc,
)
To run a simulation, we also need to specify some sources. We’re going to send a constant optical signal through the waveguide while linearly increasing the applied voltage.
def ramp_function(t_rise, amplitude):
"""Returns a simple linear voltage ramping function to apply to our circuit. "t" is the current time in the
simulation, "t_rise" is the time it takes for the voltage to ramp to its maximum, and "amplitude" is the final
value of the applied voltage.
"""
def f_step(t):
if t <= t_rise:
return amplitude * (t / t_rise)
else:
return amplitude
return f_step
dt = 1e-7 # setting up the time step variable for our simulation
voltage_function = ramp_function(t_rise=70 * dt, amplitude=3) # create our driving voltage function
# 9. We will create a constant unitary optical source, and the driving voltage using the ramp function. Then we use
# i3.ConnectComponents() to connect our component to the optical and electrical sources and an optical probe.
optical_source = i3.FunctionExcitation(port_domain=i3.OpticalDomain, excitation_function=lambda x: 1)
voltage_drive = i3.FunctionExcitation(port_domain=i3.ElectricalDomain, excitation_function=voltage_function)
Now, we can make a ‘testbench’ circuit that connects the sources to the waveguide, comparable to what you would do in a lab.
The simulation is started by instantiating the circuit model of the testbench circuit and running get_time_response.
circuit = i3.ConnectComponents(
child_cells={
"wg": HeatedWaveguideTestCell(), # the circuit we want to simulate
"src_opt": optical_source, # the optical source to be used
"v_drive": voltage_drive, # the drive voltage excitation
"opt_out_probe": i3.Probe(port_domain=i3.OpticalDomain), # our optical monitor
},
links=[
("v_drive:out", "wg:elec1"), # connect the dc_voltage to one of the electric heaters in the circuit
("src_opt:out", "wg:in"), # connect the optical source to the waveguide input
("wg:out", "opt_out_probe:in"), # connect the optical probe to the waveguide output.
],
)
# 10. We can plot the results of our time domain simulation using the get_time_response() function and some common
# Python plotting functionality. As expected, the optical power is constant as there is no loss in the model from
# applied voltage. However, there is a constant (small) propagation loss of about 0.4% due to the length. The phase
# changes quadratically with a linearly applied voltage for the first 70 time steps, where the ramp stops, at which
# point a constant phase is seen for the rest of the simulation.
result = circuit.CircuitModel().get_time_response(t0=0.0, t1=1e-5, dt=dt, center_wavelength=1.55)
The result is plotted as usual using Matplotlib:
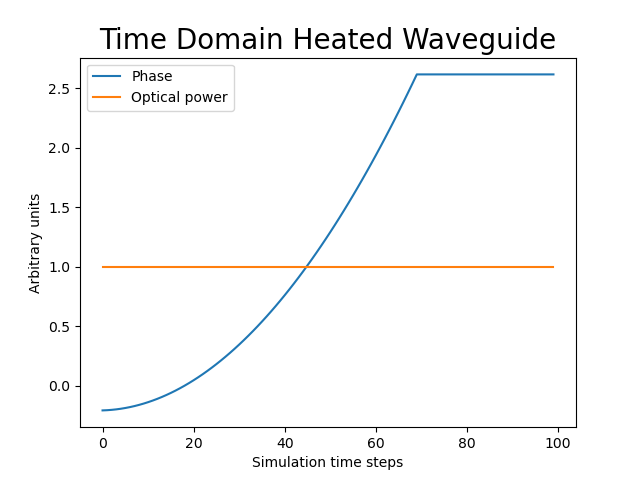
Time-domain simulation of a heated waveguide, linearly increasing the voltage across it
For more information, please visit the dedicated tutorial on circuit simulations in our documentation.